Question

在四边形ABCD中，∠ADC=∠B=90°，DE⊥AB，垂足为E，AD=CD，且DE=BE=5，请用旋转图形的方法求四边形ABCD的面积．

Answer 1

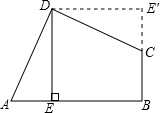解：把Rt△DEA以绕D按逆时针旋转90°，如图．
∵旋转不改变图形的形状和大小，
∴A与C重合，∠A=∠DCE′，∠E′=∠AED=90°．
在四边形ABCD中，∵∠ADC=∠B=90°，
∴∠A+∠DCB=180°；，
∴∠DCE′+∠DCB=180°，
即点B、C、E′在同一直线上；
∵∠DEB=∠E′=∠B=90°，
∴四边形DEBE′是矩形，
∴S_{矩形DEBE′}=DE×BE=5×5=25，
∵S_{矩形DEBE′}=S_{四边形DEBC}+S_△DCE，
∵S_{四边形ABCD}=S_{四边形DEBC}+S_△ADE=S_{四边形DEBC}+S_△DCE，
∴S_{四边形ABCD}=S_矩形DEBE=25．
故四边形ABCD的面积为25．
分析：根据旋转的性质将四边形ABCD变形为正方形DEBE′，易求四边形ABCD的面积．
点评：用旋转图形的方法将不规则图形转化为常见图形是数学中的一种解题思路．