Question

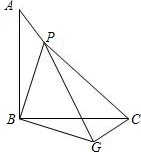如图，已知△ABP绕顶点B按顺时针方向旋转90°到△CBG，连接PG、PC，若PA=1，PB=2，PC=3．
（1）求出PG的长度；
（2）请你猜想△PGC的形状，并说明理由．

Answer 1

分析：（1）由旋转的性质可知△BPG为等腰直角三角形，即∠PBG=90°且BP=BG=2，由勾股定理可求PG的长；
（2）由旋转的性质可知CG=PA=1，已知PC=3，PG=2

2

，由勾股定理的逆定理可判断△PGC的形状．

解答：解：（1）∵△ABP绕点B顺时针旋转90°到达△CBG，
∴∠PBG=90°且BP=BG=2，
在Rt△BPG中
PG=

BP2+BG2

=

22+22

=

8

=2

2

；

（2）在△PCG中，∵GC2+PG2=1+(2

2

)2=9，（5分）
PC²=3²=9，
∴PG²+GC²=PC²，（6分）
∴△PCG是直角三角形．（7分）

点评：本题考查了旋转的性质、勾股定理及其逆定理的运用．关键是掌握线段之间的转化．