��Ŀ����
��ͼ����A��1��0����B��3��0����x��Ĵ��ߣ��ֱ�ֱ��y=4��x��C��D���㣮������y=ax2+bx+c����O��C��D���㣮
��1���������ߵı���ʽ��
��2����MΪֱ��OD�ϵ�һ�����㣬��M��x��Ĵ��߽��������ڵ�N�����Ƿ���������ĵ�M��ʹ����A��C��M��NΪ������ı���Ϊƽ���ı��Σ������ڣ����ʱ��M�ĺ����ꣻ�������ڣ���˵�����ɣ�
��3������AOC��CD����ƽ�ƣ���C���߶�CD�ϣ��Ҳ����D�غϣ�����ƽ�ƵĹ����С�AOC���OBD�ص����ֵ������ΪS������S�����ֵ��

�⣺��1�������⣬�ɵ�C��1��3����D��3��1����
�������߹�ԭ�㣬���������ߵĽ���ʽΪ��y=ax2+bx��
�� �����
����� ��
��
�������ߵı���ʽΪ��y=�� x2+
x2+ x��
x��
��2�����ڣ�
��ֱ��OD����ʽΪy=kx����D��3��1���������k= ��
��
��ֱ��OD����ʽΪy= x��
x��
���M�ĺ�����Ϊx����M��x�� x����N��x����
x����N��x���� x2+
x2+ x����
x����
��MN=|yM��yN|=| x������
x������ x2+
x2+ x��|=|
x��|=| x2��4x|��
x2��4x|��
�����⣬��֪MN��AC����Ϊ��A��C��M��NΪ������ı���Ϊƽ���ı��Σ�����MN=AC=3��
��| x2��4x|=3��
x2��4x|=3��
�� x2��4x=3�������ã�4x2��12x��9=0����ã�x=
x2��4x=3�������ã�4x2��12x��9=0����ã�x= ��x=
��x= ��
��
�� x2��4x=��3�������ã�4x2��12x+9=0����ã�x=
x2��4x=��3�������ã�4x2��12x+9=0����ã�x= ��
��
��������������ĵ�M����M�ĺ�����Ϊ�� ��
�� ��
�� ��
��
��3����C��1��3����D��3��1��
����ֱ��OC�Ľ���ʽΪy=3x��ֱ��OD�Ľ���ʽΪy= x��
x��
����ͼ��ʾ��
��ƽ���е�������Ϊ��A��O��C�䣬��C�����߶�CD�ϣ�
��O��C����x�ύ�ڵ�E����ֱ��OD���ڵ�P��
��A��C����x�ύ�ڵ�F����ֱ��OD���ڵ�Q��
��ˮƽ�����ƽ�ƾ���Ϊt��0��t��2����
��ͼ��AF=t��F��1+t����Q��1+t�� +
+ t����C�䣨1+t��3��t����
t����C�䣨1+t��3��t����
��ֱ��O��C��Ľ���ʽΪy=3x+b��
��C�䣨1+t��3��t������ã�b=��4t��
��ֱ��O��C��Ľ���ʽΪy=3x��4t��
��E�� t��0����
t��0����
����y=3x��4t��y= x�����x=
x�����x= t����P��
t����P�� t��
t�� t����
t����
����P��PG��x���ڵ�G����PG= t��
t��
��S=S��OFQ��S��OEP= OF•FQ��
OF•FQ�� OE•PG
OE•PG
= ��1+t����
��1+t���� +
+ t����
t���� •
• t•
t• t
t
=�� ��t��1��2+
��t��1��2+
��t=1ʱ��S�����ֵΪ ��
��
��S�����ֵΪ ��
��


�±��У�y��x��һ�κ�����
| x | ﹣2 | 1 | 2 | ��4�� | 5 |
| y | 6 | ﹣3 | ��﹣6�� | ﹣12 | ﹣15 |
��1����ú����ı���ʽ������ȫ����
��2����֪�ú���ͼ����һ��M��1��﹣3��Ҳ�ڷ���������y=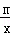 ͼ���ϣ�������������ͼ�����һ����N�����꣮
ͼ���ϣ�������������ͼ�����һ����N�����꣮
��֪���κ���y=ax2+bx+c��ͼ����ͼ��ʾ�����н��ۣ�
��abc��0����2a��b��0����4a��2b+c��0���ܣ�a+c��2��b2
������ȷ�ĸ����У�������
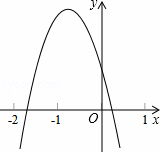
| �� | A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
��ʽ�ֽ�a2b��b����ȷ����ǣ�������
| �� | A�� | b��a+1����a��1�� | B�� | a��b+1����b��1�� | C�� | b��a2��1�� | D�� | b��a��1��2 |
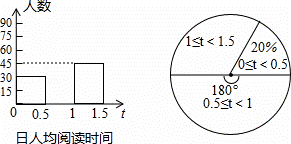

 ��ͼ���ÿһ�������ϣ�y����x���������С����k��ȡֵ��Χ�ǣ�������
��ͼ���ÿһ�������ϣ�y����x���������С����k��ȡֵ��Χ�ǣ������� ��1�ζ��ۺ�õ���ͼ�����ΪS1����2�ζ��ۺ�õ���ͼ�����ΪS2��������n�ζ��ۺ�õ���ͼ�����ΪSn�������ͼ2����S1+S2+S3+��+S2014=
��1�ζ��ۺ�õ���ͼ�����ΪS1����2�ζ��ۺ�õ���ͼ�����ΪS2��������n�ζ��ۺ�õ���ͼ�����ΪSn�������ͼ2����S1+S2+S3+��+S2014=