题目内容
 如图,扇形OAB的半径为6cm,AC切弧AB于点A,交OB的延长线点C,若AC=4cm,弧AB的长为3cm,则图中阴影部分面积为
如图,扇形OAB的半径为6cm,AC切弧AB于点A,交OB的延长线点C,若AC=4cm,弧AB的长为3cm,则图中阴影部分面积为考点:扇形面积的计算
专题:
分析:根据AC切弧AB于点A判断出CA⊥OA,再根据三角形的面积公式求出S△AOC,再求出扇形的面积,相减即可得到阴影面积.
解答:解:∵AC切弧AB于点A,
∴CA⊥OA,
∴S△AOC=
×6×4=12cm,
∵S扇形AOB=
×6×3=9cm2,
∴阴影部分面积为12-9=3cm2.
故答案为3.
∴CA⊥OA,
∴S△AOC=
| 1 |
| 2 |
∵S扇形AOB=
| 1 |
| 2 |
∴阴影部分面积为12-9=3cm2.
故答案为3.
点评:本题考查了扇形面积的计算,要灵活运用公式,同时注意切线的性质.

练习册系列答案
相关题目
下列比较大小正确的是( )
| A、(-2)3>(-2)2 | ||||
| B、-(-3)>-|-3| | ||||
| C、(-3)3>(-2)3 | ||||
D、-
|
一元二次方程x2-16=0的解是( )
| A、x1=2,x2=-2 |
| B、x1=4,x2=-4 |
| C、x1=8,x2=-8 |
| D、x1=16,x2=-16 |
 如图,点O在△ABC内,且到三边的距离相等,若∠A=60°,则∠BOC的大小为( )
如图,点O在△ABC内,且到三边的距离相等,若∠A=60°,则∠BOC的大小为( )| A、135° | B、120° |
| C、90° | D、60° |
若-2a3b与5anbm+n可以合并成一项,则mn的值是( )
| A、-6 | B、8 | C、-8 | D、6 |
一次函数y=-4x+8的图象不经过的象限是( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
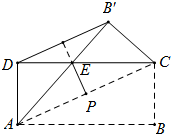 如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′的位置,AB′与CD相交于点E,连接B′D.若P为AC的中点,求证:PE⊥B′D.
如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′的位置,AB′与CD相交于点E,连接B′D.若P为AC的中点,求证:PE⊥B′D. 如图,O为△ABC的重心,若OD=2,则AO=
如图,O为△ABC的重心,若OD=2,则AO= 如图,在△ABC中,AD=DC,BE=EF=CF,AE、CF与BD相交于点G、H.已知S△ABC=
如图,在△ABC中,AD=DC,BE=EF=CF,AE、CF与BD相交于点G、H.已知S△ABC=