题目内容
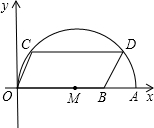 (1)如图,在平面直角坐标系中,点A的坐标是(10,0),点B的坐标为(8,0),点C、D在以OA为直径的半圆M上,且四边形OCDB是平行四边形.求点C的坐标.
(1)如图,在平面直角坐标系中,点A的坐标是(10,0),点B的坐标为(8,0),点C、D在以OA为直径的半圆M上,且四边形OCDB是平行四边形.求点C的坐标.(2)在(1)的条件下,试在直角坐标系内确定点N,使△NOA与△AOC相似,求出所有符合条件的点N的坐标.
分析:(1)过C作CE⊥OA,利用平行四边形的性质得出,C点的横纵坐标;
(2)利用相似三角形的判定,根据△AOC三边长度,得出△NOA三边长度,从而得出所有符合条件的点N的坐标.
(2)利用相似三角形的判定,根据△AOC三边长度,得出△NOA三边长度,从而得出所有符合条件的点N的坐标.
解答: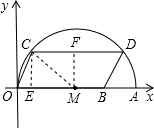 解:(1)∵四边形OCDB是平行四边形,B(8,0),
解:(1)∵四边形OCDB是平行四边形,B(8,0),
∴CD∥OA,CD=OB=8,过点M作MF⊥CD于点F,
则CF=
CD=4,
过点C作CE⊥OA于点E,
∵A(10,0),
∴OE=OM-ME=OM-CF=5-4=1,
连接MC,则MC=
OA=5,
∴在RT△CMF中,MF=3,
∴点C的坐标为(1,3);
(2)使△NOA与△AOC相似,
N1(1,-3),N2(9,3),N3(9,-3),N4(10,30),N5(10,-30),N6(10,
),N7(10,-
).
 解:(1)∵四边形OCDB是平行四边形,B(8,0),
解:(1)∵四边形OCDB是平行四边形,B(8,0),∴CD∥OA,CD=OB=8,过点M作MF⊥CD于点F,
则CF=
| 1 |
| 2 |
过点C作CE⊥OA于点E,
∵A(10,0),
∴OE=OM-ME=OM-CF=5-4=1,
连接MC,则MC=
| 1 |
| 2 |
∴在RT△CMF中,MF=3,
∴点C的坐标为(1,3);
(2)使△NOA与△AOC相似,
N1(1,-3),N2(9,3),N3(9,-3),N4(10,30),N5(10,-30),N6(10,
| 10 |
| 3 |
| 10 |
| 3 |
点评:此题主要考查了相似三角形的性质与判定以及平行四边形的性质等知识,利用平行四边形的性质得出C点坐标,注意构建直角三角形求出是解决问题的关键.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 四边形是平行四边形.
四边形是平行四边形. 如图,在平面直角坐标系中,直
如图,在平面直角坐标系中,直 如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(-2,4),过点A作AB⊥y轴,垂足为B,连接OA.
如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(-2,4),过点A作AB⊥y轴,垂足为B,连接OA.
 如图,在平面直角坐标系中,原点O处有一乒乓球发射器向空中发射乒乓球,乒乓球飞行路线是一条抛物线,在地面上落点落在X轴上为点B.有人在线段OB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让乒乓球落入桶内.已知OB=4米,OC=3米,乒乓球飞行最大高度MN=5米,圆柱形桶的直径为0.5,高为0.3米(乒乓球的体积和圆柱形桶的厚度忽略不计).
如图,在平面直角坐标系中,原点O处有一乒乓球发射器向空中发射乒乓球,乒乓球飞行路线是一条抛物线,在地面上落点落在X轴上为点B.有人在线段OB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让乒乓球落入桶内.已知OB=4米,OC=3米,乒乓球飞行最大高度MN=5米,圆柱形桶的直径为0.5,高为0.3米(乒乓球的体积和圆柱形桶的厚度忽略不计).