题目内容
【题目】在正方形ABCD中，对角线AC、BD交于点O，点P在线段BC上（不与点B重合），E在BO上，且∠BPE=
，过点B作PE交PE的延长线于F，交AC于点G．
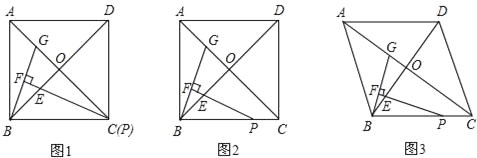
（1）当点P与点C重合时（如图1），填空△BOG≌_________，
=_________；
（2）当点P不与点C重合时（图2），猜想：的值为_________．并证明你的结论；
（3）把正方形ABCD改为菱形，其他条件不变（如图3），若∠ACB=α，则直接写出的值．
【答案】（1）△POE，
；（2）；（3）
tanα．
【解析】
试题分析：（1）∵四边形ABCD是正方形，P与C重合，∴OB=OP，∠BOC=∠BOG=90°．∵PF⊥BG，∠PFB=90°，∴∠GBO=90°﹣∠BGO，∠EPO=90°﹣∠BGO．∴∠GBO=∠EPO．∴△BOG≌△POE（AAS）．∴PE=BG，∵∠BPE=
，∴∠BPE=∠GPF，∵PF⊥BG，∴BF=BG，∴
=，故答案为△POE，；
（2）证明如下：如图2，
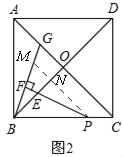
过P作PM∥AC交BG于M，交BO于N，∴∠PNE=∠BOC=90°，∠BPN=∠OCB．∵∠OBC=∠OCB=45°，∴∠NBP=∠NPB．∴NB=NP．∵∠MBN=90°﹣∠BMN，∠NPE=90°﹣∠BMN，∴∠MBN=∠NPE．∴△BMN≌△PEN（ASA）．∴BM=PE．∵∠BPE=∠ACB，∠BPN=∠ACB，∴∠BPF=∠MPF．∵PF⊥BM，∴∠BFP=∠MFP=90°．∵PF=PF，∴△BPF≌△MPF（ASA）．∴BF=MF，即BF=BM．∴BF=PE，即：
=
．故答案为；
（3）如图2，过P作PM∥AC交BG于点M，交BO于点N，
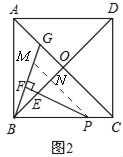
∴∠BPN=∠ACB=α，∠PNE=∠BOC=90°．由（2）同理可得，BF=BM，∠MBN=∠EPN． ∵∠BNM=∠PNE=90°，∴△BMN∽△PEN．∴
．在Rt△BNP中，tanα=
，∴
=tanα，即：
=tanα．∴
=tanα．
