题目内容
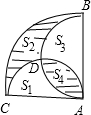如图，在直角扇形ABC内，分别以AB和AC为直径作半圆，两条半圆弧相交于点D，整个图形被分成S1，S2，S3，S4四部分，则S2和S4的大小关系是
- A.S2＜S4
- B.S2=S4
- C.S2＞S4
- D.无法确定
B
分析：设AB=AC=2a，由S2=S扇形ACB-S半圆AB-S半圆AC+S4，根据扇形和圆的面积公式分别计算出它们的面积就可得到S2和S4的大小关系．
解答：设AB=AC=2a，根据题意得，
S2=S扇形ACB-S半圆AB-S半圆AC+S4=
-2×
×π×a2+S4=S4，
所以S2=S4．
故选B．
点评：本题考查了扇形的面积公式：S=
，其中n为扇形的圆心角的度数，R为圆的半径），或S=lR，l为扇形的弧长，R为半径．
分析：设AB=AC=2a，由S2=S扇形ACB-S半圆AB-S半圆AC+S4，根据扇形和圆的面积公式分别计算出它们的面积就可得到S2和S4的大小关系．
解答：设AB=AC=2a，根据题意得，
S2=S扇形ACB-S半圆AB-S半圆AC+S4=
-2××π×a2+S4=S4，所以S2=S4．
故选B．
点评：本题考查了扇形的面积公式：S=
，其中n为扇形的圆心角的度数，R为圆的半径），或S=lR，l为扇形的弧长，R为半径． 
练习册系列答案
相关题目
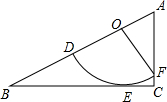如图所示为扇形DOF与直角△ABC的重迭情形，其中O，D，F分别在AB，OB，AC上，且
x上，AB边在直线y＝－
x＋
上．