题目内容

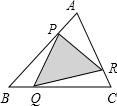如图所示，△ABC中，点P在边AB上，AP= $数学公式$ AB，Q点在边BC上，BQ= $数学公式$ ，R点在CA边上，CR= $数学公式$ CA，已知阴影△PQR的面积是19平方厘米，那么△ABC的面积是________平方厘米．

45.6
分析：利用三角形的面积与边长之间的关系，求出阴影部分面积与三角形ABC的关系，代入阴影部分的面积即可求出△ABC的面积．
解答：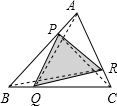

解：如图所示，连接AQ，则有△ABQ．
∵BQ= $\text{[math]}$ BC，
∴S_△ABQ= $\text{[math]}$ S_△ABC，又AP= $\text{[math]}$ AB，
∴S_△PBQ= $\text{[math]}$ S_△ABQ= $\text{[math]}$ × $\text{[math]}$ S_△ABC= $\text{[math]}$ S_△ABC．
连接BR，
∵RC= $\text{[math]}$ AC，
∴S_△BCR= $\text{[math]}$ S_△ABC，
又∵BQ= $\text{[math]}$ BC，
∴S_△QCR= $\text{[math]}$ S_△BCR= $\text{[math]}$ S_△ABC．
连接CP，
∵AP= $\text{[math]}$ AB，
∴S_△ACP= $\text{[math]}$ S_△ABC，
又∵RC= $\text{[math]}$ AC，
∴S_△APR= $\text{[math]}$ S_△ACP= $\text{[math]}$ S_△ABC．
即：S_△PBQ+S_△QCR+S_△APR=（ $\text{[math]}$ + $\text{[math]}$ + $\text{[math]}$ ）S_△ABC= $\text{[math]}$ S_△ABC，
S_阴影△PQR=（1- $\text{[math]}$ ）S_△ABC= $\text{[math]}$ S_△ABC=19，
∴S_△ABC= $\text{[math]}$ ×19=45.6（平方厘米）．
故答案为45.6．
点评：本题主要考查了三角形面积公式的灵活应用，关键在于找出阴影部分的面积与△ABC的面积之间的关系．