题目内容
 如图,AB是⊙O的切线,切点为A,OB与⊙O交于C,且点C为OB的中点,过C点作弦CD使∠ACD=45°,弧AD的长为
如图,AB是⊙O的切线,切点为A,OB与⊙O交于C,且点C为OB的中点,过C点作弦CD使∠ACD=45°,弧AD的长为 π,则以AD和AC的长为两根的一元二次方程是
π,则以AD和AC的长为两根的一元二次方程是
- A.x2-(2+
 )x+2
)x+2 =0
=0 - B.x2-(2+
 )x-2
)x-2 =0
=0 - C.x2-(2-
 )x+2
)x+2 =0
=0 - D.x2-(2-
 )x-2
)x-2 =0
=0
A
分析:连OA、OD,设⊙O半径为R,根据圆周角定理得到∠AOD=2∠ACD=90°,则△AOD为等腰直角三角形,再利用弧长公式有 =
= π,解得R=
π,解得R= ,则AD=
,则AD= OD=
OD= ×
× =2,然后根据切线的性质得OA⊥AB,即∠OAB=90°,而点C为OB的中点,根据直角三角形斜边上的中线等于斜边的一半得到AC=
=2,然后根据切线的性质得OA⊥AB,即∠OAB=90°,而点C为OB的中点,根据直角三角形斜边上的中线等于斜边的一半得到AC= BC=OC=
BC=OC= ,根据根与系数的关系可得以2和
,根据根与系数的关系可得以2和 为根的一元二次方程可为(x-2)(x-
为根的一元二次方程可为(x-2)(x- )=0,化为一般式为:x2-(2+
)=0,化为一般式为:x2-(2+ )x+2
)x+2 =0.
=0.
解答:连OA、OD,如图,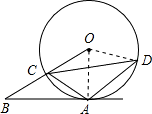 设⊙O半径为R,
设⊙O半径为R,
∵∠ACD=45°,
∴∠AOD=2∠ACD=90°,则△AOD为等腰直角三角形,
∴弧AD的长= ,
,
而弧AD的长为 π,
π,
∴ =
= π,解得R=
π,解得R= ,
,
∴AD= OD=
OD= ×
× =2,
=2,
又∵AB是⊙O的切线,
∴OA⊥AB,即∠OAB=90°,
∵点C为OB的中点,
∴AC= BC=OC=
BC=OC= ,
,
∴以2和 为根的一元二次方程可为(x-2)(x-
为根的一元二次方程可为(x-2)(x- )=0,
)=0,
化为一般式为:x2-(2+ )x+2
)x+2 =0.
=0.
故选A.
点评:本题考查了切线的性质:圆的切线垂直于过切点的半径.也考查了圆周角定理、弧长公式、直角三角形斜边上的中线性质以及一元二次方程根与系数的关系.
分析:连OA、OD,设⊙O半径为R,根据圆周角定理得到∠AOD=2∠ACD=90°,则△AOD为等腰直角三角形,再利用弧长公式有
 =
= π,解得R=
π,解得R= ,则AD=
,则AD= OD=
OD= ×
× =2,然后根据切线的性质得OA⊥AB,即∠OAB=90°,而点C为OB的中点,根据直角三角形斜边上的中线等于斜边的一半得到AC=
=2,然后根据切线的性质得OA⊥AB,即∠OAB=90°,而点C为OB的中点,根据直角三角形斜边上的中线等于斜边的一半得到AC= BC=OC=
BC=OC= ,根据根与系数的关系可得以2和
,根据根与系数的关系可得以2和 为根的一元二次方程可为(x-2)(x-
为根的一元二次方程可为(x-2)(x- )=0,化为一般式为:x2-(2+
)=0,化为一般式为:x2-(2+ )x+2
)x+2 =0.
=0.解答:连OA、OD,如图,
 设⊙O半径为R,
设⊙O半径为R,∵∠ACD=45°,
∴∠AOD=2∠ACD=90°,则△AOD为等腰直角三角形,
∴弧AD的长=
 ,
,而弧AD的长为
 π,
π,∴
 =
= π,解得R=
π,解得R= ,
,∴AD=
 OD=
OD= ×
× =2,
=2,又∵AB是⊙O的切线,
∴OA⊥AB,即∠OAB=90°,
∵点C为OB的中点,
∴AC=
 BC=OC=
BC=OC= ,
,∴以2和
 为根的一元二次方程可为(x-2)(x-
为根的一元二次方程可为(x-2)(x- )=0,
)=0,化为一般式为:x2-(2+
 )x+2
)x+2 =0.
=0.故选A.
点评:本题考查了切线的性质:圆的切线垂直于过切点的半径.也考查了圆周角定理、弧长公式、直角三角形斜边上的中线性质以及一元二次方程根与系数的关系.

练习册系列答案
相关题目
 12、已知,如图,AB是⊙O的直径,DC切⊙O于点C,AB=2BC,则∠BCD=
12、已知,如图,AB是⊙O的直径,DC切⊙O于点C,AB=2BC,则∠BCD= 如图,AB是⊙O的直径,点C在AB的延长线上,CD切⊙O于点D,过点D作DF⊥AB于点E,交⊙O于点F,OE=1cm,DF=2cm,则CB的长为( )
如图,AB是⊙O的直径,点C在AB的延长线上,CD切⊙O于点D,过点D作DF⊥AB于点E,交⊙O于点F,OE=1cm,DF=2cm,则CB的长为( )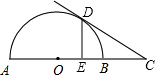
 21、如图,AB是⊙O的直径,AC是弦,直线CE和⊙O切于点C,AD⊥CE,垂足为D.求证:AC平分∠BAD.
21、如图,AB是⊙O的直径,AC是弦,直线CE和⊙O切于点C,AD⊥CE,垂足为D.求证:AC平分∠BAD. 如图,AB是半圆的直径,直线MN切半圆于点C,AM⊥MN,BN⊥MN,如果AM=a,BN=b,那么半圆的直径为
如图,AB是半圆的直径,直线MN切半圆于点C,AM⊥MN,BN⊥MN,如果AM=a,BN=b,那么半圆的直径为