题目内容
 已知△ABC及BC边上的中点O,
已知△ABC及BC边上的中点O,(1)将△ABC中的顶点A绕着O点顺时针旋转180°后得到点A′,连接BA′、CA′,得到四边形ABA′C,请在图中画出这个四边形.则这个四边形是
平行四边形
平行四边形
,你判断的理由是对角线互相平分的四边形是平行四边形
对角线互相平分的四边形是平行四边形
.(2)若要使四边形ABA′C为菱形,则△ABC应满足条件:
AB=AC
AB=AC
.(3)若要使四边形ABA′C为正方形,则△ABC应满足条件:
AB=AC且∠A=90°
AB=AC且∠A=90°
.分析:(1)旋转中心为点O,旋转角为180°,根据旋转的性质可知,OA=OA′,已知OB=OC,根据平行四边形的判定定理得四边形ABA′C为平行四边形;
(2)根据两邻边相等的平行四边形是菱形,添加条件;
(3)根据有一个角为直角的菱形为正方形,在(2)的条件基础上增加∠A=90°.
(2)根据两邻边相等的平行四边形是菱形,添加条件;
(3)根据有一个角为直角的菱形为正方形,在(2)的条件基础上增加∠A=90°.
解答: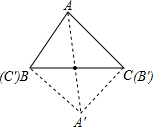 解:(1)由旋转的性质及OB=OC,可知这个四边形是平行四边形,
解:(1)由旋转的性质及OB=OC,可知这个四边形是平行四边形,
判断的理由是:对角线互相平分的四边形是平行四边形;
故答案为:平行四边形,对角线互相平分的四边形是平行四边形;
(2)△ABC应满足条件:AB=AC;
故答案为:AB=AC.
(3)△ABC应满足条件:AB=AC且∠A=90°;
故答案为:AB=AC且∠A=90°.
 解:(1)由旋转的性质及OB=OC,可知这个四边形是平行四边形,
解:(1)由旋转的性质及OB=OC,可知这个四边形是平行四边形,判断的理由是:对角线互相平分的四边形是平行四边形;
故答案为:平行四边形,对角线互相平分的四边形是平行四边形;
(2)△ABC应满足条件:AB=AC;
故答案为:AB=AC.
(3)△ABC应满足条件:AB=AC且∠A=90°;
故答案为:AB=AC且∠A=90°.
点评:本题考查了旋转的性质,平行四边形、菱形、正方形的判断.关键是根据旋转180°后的图形与原图形构成中心对称图形,再根据特殊平行四边形的判定定理添加条件.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
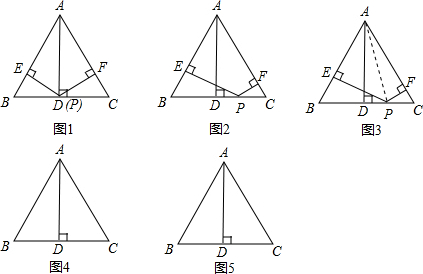 画出示意图,写出你提出的问题,并直接写出结论,不必证明.
画出示意图,写出你提出的问题,并直接写出结论,不必证明. 13、如图,已知△ABC及AB边上任意一点D,DE∥BC,交AC于E,平行四边形DEFG的边GF在直线BC上,设DE=x,BC=a,求证:平行四边形DEFG的面积S不大于△ABC的面积的一半.
13、如图,已知△ABC及AB边上任意一点D,DE∥BC,交AC于E,平行四边形DEFG的边GF在直线BC上,设DE=x,BC=a,求证:平行四边形DEFG的面积S不大于△ABC的面积的一半.

