题目内容
如图，点O为平面直角坐标系的原点，边长为4的菱形OABC的一边OA与x轴的正半轴重合，点B和点C都在第一象限，∠COA=60º，过点C的直线将菱形OABC分成面积比为1：3的两部分，求该直线的解析式。
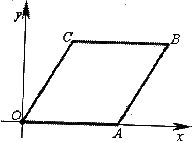
解：如图，连结AC，作CE⊥OA于点E，CF⊥AB于F，设菱形ABCO的面积为S
∴四边形ABCO是边长为4的菱形，∠COA=60º，
∴△OAC和△BAC都是等边三角形，点A的坐标为(4，0)，
∴△OAC≌△BAC，E、F分别是OA、AB的中点，
∴OE=2,CE=
，
S△COE=
S△AOC=
S△BCF=S△ABC=
∴点C的坐标为（2，2
），
S△COE ：SCEAB=1：3
S△BCF：SCFAO=1：3
∴直线CE和CF均将菱形OABC分成面积比为1：3的两部分
直线CE的解析式为x=2
∵BC//OA，BC=4
∴点B的坐标为（6，2），
∴点F的坐标为（5，），
∴可求得直线CF的解析式为：
∴所求直线的解析式为
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
BCD某一边的交点，设点B的坐标为（t，0），线段OE的长度为m．
60度．
60度．