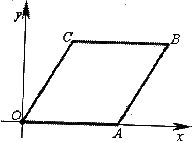
题目内容
如图,点O为平面直角坐标系的原点,边长为4的菱形OABC的一边OA与x轴的正半轴重合,∠COA= 60度.
60度.(1)求B点的坐标;
(2)过点C的直线将菱形OABC分成面积比为1:3的两部分,求该直线的解析式.
分析:(1)作CE⊥OA于点E,根据直角三角形的性质可求出B点坐标;
(2)连接AC,作CE⊥OA于点E,CF⊥AB于F,设菱形ABCO的面积为S,根据菱形的性质可求出A点的坐标,及E,F分别是OA,AB的中点,根据三角形的面积公式可求出S△COE:SCEAB=1:3,S△BCF:SCFAO=1:3,由F是AB的中点F点的坐标,用待定系数法求出直线CF的解析式.
(2)连接AC,作CE⊥OA于点E,CF⊥AB于F,设菱形ABCO的面积为S,根据菱形的性质可求出A点的坐标,及E,F分别是OA,AB的中点,根据三角形的面积公式可求出S△COE:SCEAB=1:3,S△BCF:SCFAO=1:3,由F是AB的中点F点的坐标,用待定系数法求出直线CF的解析式.
解答:解:(1)作CE⊥OA于点E
∵∠COA=60°
∴OE=
OC=
×4=2
故B点坐标为(6,2
)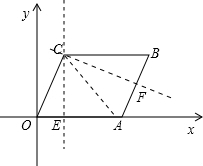
(2)如图,
连接AC,作CE⊥OA于点E,CF⊥AB于F,设菱形ABCO的面积为S
∵四边形ABCO是边长为4的菱形,∠COA=60°
∴△OAC和△BAC都是等边三角形,点A的坐标为(4,0)
∴△OAC≌△BAC,E、F分别是OA、AB的中点
∴OE=2,CE=2
,S△COE=
S△AOC=
S,S△BCF=
S△ABC=
S
∴点C的坐标为(2,2
),S△COE:SCEAB=1:3,S△BCF:SCFAO=1:3
∴直线CE和CF均将菱形OABC分成面积比为1:3的两部分,
且直线CE的解析式为x=2(7分)
∵点B的坐标为(6,2
)
∴点F的坐标为(5,
)
∴可求得直线CF的解析式为:y=-
x+
∴所求直线的解析式为x=2或y=-
x+
∵∠COA=60°
∴OE=
| 1 |
| 2 |
| 1 |
| 2 |
故B点坐标为(6,2
| 3 |

(2)如图,
连接AC,作CE⊥OA于点E,CF⊥AB于F,设菱形ABCO的面积为S
∵四边形ABCO是边长为4的菱形,∠COA=60°
∴△OAC和△BAC都是等边三角形,点A的坐标为(4,0)
∴△OAC≌△BAC,E、F分别是OA、AB的中点
∴OE=2,CE=2
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
∴点C的坐标为(2,2
| 3 |
∴直线CE和CF均将菱形OABC分成面积比为1:3的两部分,
且直线CE的解析式为x=2(7分)
∵点B的坐标为(6,2
| 3 |
∴点F的坐标为(5,
| 3 |
∴可求得直线CF的解析式为:y=-
| ||
| 3 |
8
| ||
| 3 |
∴所求直线的解析式为x=2或y=-
| ||
| 3 |
8
| ||
| 3 |
点评:本题比较复杂,涉及到菱形的性质,用待定系数法求一次函数的解析式的运用.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
 BCD某一边的交点,设点B的坐标为(t,0),线段OE的长度为m.
BCD某一边的交点,设点B的坐标为(t,0),线段OE的长度为m. 60度.
60度.