题目内容
一列数x1，x2，x3，…，其中x1=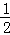
，xn=
（n为不小于2的整数），则x2015= ．
2 ．
【考点】规律型：数字的变化类．
【专题】规律型．
【分析】根据表达式求出前几个数不难发现，每三个数为一个循环组依次循环，用2015除以3，根据商和余数的情况确定a2015的值即可．
【解答】解：根据题意得，x2=
=2，
x3=
=﹣1，
x4=
=，
…，
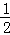依此类推，每三个数为一个循环组依次循环，
∵2015÷3=671…2，
∴x2015是第672个循环组的第2个数，与x2相同，
即x2015=2．
故答案为：2．
【点评】本题考查数字的变化规律，计算并观察出每三个数为一个循环组依次循环是解题的关键．
练习册系列答案
相关题目
的图象上的概率是 ．
x+1，当自变量x取m时，对应的函数值大于0，设自变量分别取m﹣3，m+3时对应的函数值为y1，y2，则下列判断正确的是（ ）
