题目内容
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),交
的左侧),交![]() 轴于点
轴于点![]() ,将直线
,将直线![]() 以点
以点![]() 为旋转中心,顺时针旋
为旋转中心,顺时针旋![]() 转,交
转,交![]() 轴于点
轴于点![]() ,交抛物线于另一点
,交抛物线于另一点![]() .直线
.直线![]() 的解析式为:
的解析式为:![]()
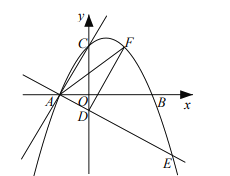
![]() 点
点![]() 是第一象限内抛物线上一点,当
是第一象限内抛物线上一点,当![]() 的面积最大时,在线段
的面积最大时,在线段![]() 上找一点
上找一点![]() (不与
(不与![]() 重合),使
重合),使![]() 的值最小,求出点
的值最小,求出点![]() 的坐标,并直接写出
的坐标,并直接写出![]() 的最小值;
的最小值;
![]() 如图,将
如图,将![]() 沿射线
沿射线![]() 方向以每秒
方向以每秒![]() 个单位的速度平移,记平移后的
个单位的速度平移,记平移后的![]() 为
为![]() ,平移时间为
,平移时间为![]() 秒,当
秒,当![]() 为等腰三角形时,求
为等腰三角形时,求![]() 的值.
的值.

【答案】(1)点![]() 的坐标为
的坐标为![]() .
.![]() 的最小值为
的最小值为![]() .(2)
.(2)![]() 或
或![]() 或
或![]() 或
或![]()
【解析】
![]() 过点
过点![]() 作
作![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.
设点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的坐标为
的坐标为![]() ,表示出FK,
,表示出FK,![]() ,根据二次函数的性质即可求解.
,根据二次函数的性质即可求解.
![]() 连接
连接![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,则
,则![]() ,
,![]() ,
,![]() .点
.点![]() 的坐标为
的坐标为![]() .求出点
.求出点![]() 的坐标为
的坐标为![]() .
.
![]()
![]() ,
,![]() ,分三种情况进行讨论即可.
,分三种情况进行讨论即可.
解:![]() 过点
过点![]() 作
作![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() (如答图1),
(如答图1),
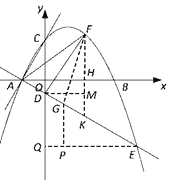
过点![]() 作
作![]() 于点
于点![]() .
.
设点![]() 的坐标为
的坐标为![]() ,
,
则点![]() 的坐标为
的坐标为![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
![]() ,
,
![]() ,
,
![]() 当
当![]() 时,
时,![]() 有最大值.
有最大值.
![]() 此时点
此时点![]() 的坐标为
的坐标为![]() .
.
点![]() 是线段
是线段![]() 上一点,作
上一点,作![]() 轴于点
轴于点![]() ,
,![]() 于点
于点![]() ,
,
则![]() ,
,![]() ,
,![]() .
.
过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 于点
于点![]() ,此时
,此时![]() 的值最小,
的值最小,
![]() 此时点
此时点![]() 的坐标为
的坐标为![]() .
.
![]() 的最小值为
的最小值为![]() .
.
![]() 连接
连接![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() (如答图2)
(如答图2)
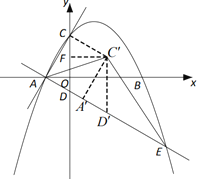
则![]() ,
,![]() ,
,![]() .
.
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
求出点![]() 的坐标为
的坐标为![]() .
.
![]()
![]()
![]() ,
,
![]() 当
当![]() 时,
时,
![]() ,解得
,解得![]() .
.
![]() 当
当![]() 时,
时,
![]() ,解得
,解得![]() (舍去)
(舍去)
![]() 当
当![]() 时,
时,
![]() ,解得
,解得![]() ,
,
综上所述,当![]() 为等腰三角形时,
为等腰三角形时,![]() 或
或![]() 或
或![]() 或
或![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目