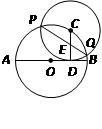题目内容
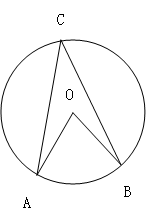
如图 是
是 的切线,
的切线, 为切点,
为切点, 是
是 的直径,
的直径, ,则
,则 的度数是( )
的度数是( )

 是
是 的切线,
的切线, 为切点,
为切点, 是
是 的直径,
的直径, ,则
,则 的度数是( )
的度数是( )
A. | B. | C. | D. |
B
分析:连接BC,OB,根据圆周角定理先求出∠C,再求∠BAC.
解答:解:连接BC,OB,

AC是直径,则∠ABC=90°,
PA、PB是⊙O的切线,A、B为切点,则∠OAP=∠OBP=90°,
∴∠AOB=180°-∠P=140°,
由圆周角定理知,∠C= ∠AOB=70°,
∠AOB=70°,
∴∠BAC=90°-∠C=20°.
故选B.
解答:解:连接BC,OB,

AC是直径,则∠ABC=90°,
PA、PB是⊙O的切线,A、B为切点,则∠OAP=∠OBP=90°,
∴∠AOB=180°-∠P=140°,
由圆周角定理知,∠C=
 ∠AOB=70°,
∠AOB=70°,∴∠BAC=90°-∠C=20°.
故选B.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的图象上运动,当⊙P与x轴相切时,点P的坐标是 .
的图象上运动,当⊙P与x轴相切时,点P的坐标是 .
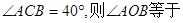 ( )
( )
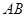 为
为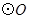 的直径,
的直径,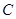 为
为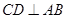 于
于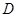 .
.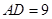 、
、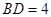 ,以
,以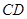 为半径的圆与
为半径的圆与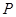 、
、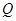 两点,弦
两点,弦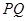 交
交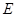 .则
.则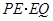 的值是( )
的值是( )