题目内容
如图,已知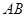 为
为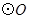 的直径,
的直径,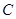 为
为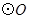 上一点,
上一点,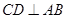 于
于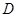 .
.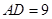 、
、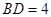 ,以
,以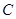 为圆心,
为圆心,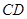 为半径的圆与
为半径的圆与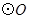 相交于
相交于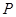 、
、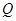 两点,弦
两点,弦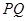 交
交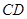 于
于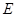 .则
.则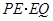 的值是( )
的值是( )
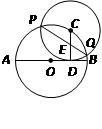
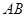 为
为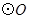 的直径,
的直径,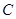 为
为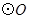 上一点,
上一点,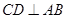 于
于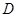 .
.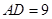 、
、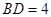 ,以
,以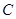 为圆心,
为圆心,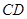 为半径的圆与
为半径的圆与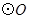 相交于
相交于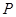 、
、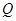 两点,弦
两点,弦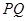 交
交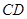 于
于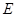 .则
.则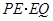 的值是( )
的值是( )| A.24 | B.9 | C.36 | D.27 |
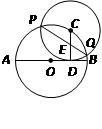
D
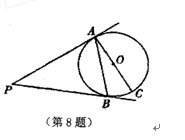
分析:延长DC交⊙C于M,延长CD交⊙O于N.在⊙O中,由垂径定理、相交弦定理易得CD=6.在⊙O、⊙C中,由相交弦定理可知PE?EQ=DE?EM=CE?EN,设CE=x,列方程求解得CE=3.所以DE=6-3=3,EM=6+3=9,即可求得PE?EQ.
解答:解:延长DC交⊙C于M,延长CD交⊙O于N.

∵CD2=AD?DB,AD=9,BD=4,
∴CD=6.
在⊙O、⊙C中,由相交弦定理可知,PE?EQ=DE?EM=CE?EN,
设CE=x,则DE=6-x,
则(6-x)(x+6)=x(6-x+6),
解得x=3.
所以,CE=3,DE=6-3=3,EM=6+3=9.
所以PE?EQ=3×9=27.
故选D.
解答:解:延长DC交⊙C于M,延长CD交⊙O于N.

∵CD2=AD?DB,AD=9,BD=4,
∴CD=6.
在⊙O、⊙C中,由相交弦定理可知,PE?EQ=DE?EM=CE?EN,
设CE=x,则DE=6-x,
则(6-x)(x+6)=x(6-x+6),
解得x=3.
所以,CE=3,DE=6-3=3,EM=6+3=9.
所以PE?EQ=3×9=27.
故选D.

练习册系列答案
相关题目
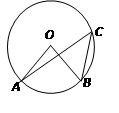
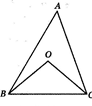
 的半径为6cm,⊙O
的半径为6cm,⊙O 的半径是2cm,O
的半径是2cm,O 是
是 的切线,
的切线, 为切点,
为切点, 是
是 ,则
,则 的度数是( )
的度数是( )