Question

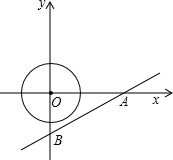
如图，直线l的解析式为y=-

1

3

x+5，点A（m，0）为x轴上一动点，过A作直线AB⊥x轴，交直线l于B，以线段AB为直径作⊙P，当m=

15

7

或-3

时，⊙P与两坐标轴都相切．

Answer 1

分析：本题需要分两类情况讨论，①点P在x轴左边，②点P在x轴右边，根据△CDO∽△CBA，利用相似三角形的对应边成比例，可求出m的值．

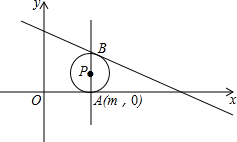
解答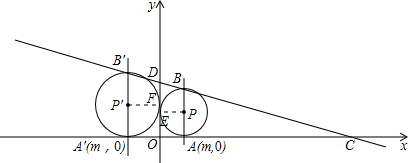：解：①当点P在x轴右边，⊙P与两坐标轴相切时，此时m＞0，如图所示：
∵直线l解析式为y=-

1

3

x+5，
∴OC=15，OD=5，
⊙P的半径为m，则AB=2m，
易得△CDO∽△CBA，
∴

AB

OD

=

AC

OC

，即

2m

5

=

15-m

15

，
解得：m=

15

7

；

②当点P在x轴左边，⊙P与两坐标轴相切时，此时m＜0，如图所示：
⊙P的半径长=P'F=-m，则A'B'=-2m，
易得△△CDO∽△CB'A'，
∴

A′B′

OD

=

A′C

OC

，即

-2m

5

=

15-m

15

，
解得：m=-3；
综上可得：当m=

15

7

或-3时，⊙P与两坐标轴都相切．
故答案为：

15

7

或-3．

点评：本题考查了圆的综合，解答此类题目关键是画出示意图，运用数形结合思想求解，注意本题应分两种情况讨论，很容易漏解．