题目内容
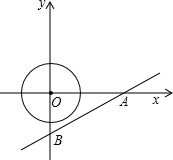 如图,直线l的解析式为y=
如图,直线l的解析式为y=| 3 | 4 |
(1)求A,B两点的坐标;
(2)一个圆心在坐标原点、半径为1的圆,以0.4个单位/s的速度向x轴正方向运动,问在什么时刻该圆与直线l相切?
分析:(1)根据题意可将A,B代入解析式中求出两点坐标;
(2)当圆与直线相切时,根据直线1与x轴的角度可求出圆心坐标,然后再求出时间t.
(2)当圆与直线相切时,根据直线1与x轴的角度可求出圆心坐标,然后再求出时间t.
解答:解:如图所示:
(1)在y=
x-3中,令x=0,得y=-3;令y=0,
得x=4,
故A,B两点的坐标分别为A(4,0),B(0,-3).
(2)若动圆的圆心在C处时与直线l相切,设切点为D,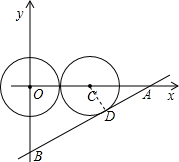
如图所示,连接CD,则CD⊥AD.由∠CAD=∠BAO,∠CDA=∠BOA=90°,
可知Rt△ACD∽Rt△ABO.
∴
=
,即
=
,则AC=
.
此时OC=4-
=
,t=
=
÷0.4=
(s).
根据对称性,圆C还可能在直线l的右侧,与直线相切,
此时OC=4+
=
,t=
=
÷0.4=
(s).
∴t=
s或t=
s时圆与直线l相切.
(1)在y=
| 3 |
| 4 |
得x=4,
故A,B两点的坐标分别为A(4,0),B(0,-3).
(2)若动圆的圆心在C处时与直线l相切,设切点为D,

如图所示,连接CD,则CD⊥AD.由∠CAD=∠BAO,∠CDA=∠BOA=90°,
可知Rt△ACD∽Rt△ABO.
∴
| CD |
| BO |
| AC |
| AB |
| 1 |
| 3 |
| AC |
| 5 |
| 5 |
| 3 |
此时OC=4-
| 5 |
| 3 |
| 7 |
| 3 |
| s |
| v |
| 7 |
| 3 |
| 35 |
| 6 |
根据对称性,圆C还可能在直线l的右侧,与直线相切,
此时OC=4+
| 5 |
| 3 |
| 17 |
| 3 |
| s |
| v |
| 17 |
| 3 |
| 85 |
| 6 |
∴t=
| 35 |
| 6 |
| 85 |
| 6 |
点评:本题主要考查对于一次函数的应用以及对于圆和直线相切的性质的认识.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
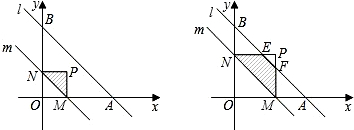

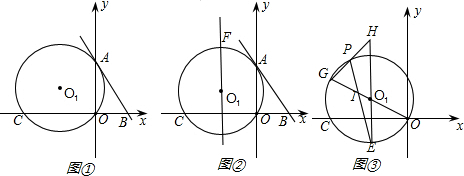
 如图,直线AB的解析式为y=
如图,直线AB的解析式为y= 求如图中直线L的解析式.
求如图中直线L的解析式.