题目内容
如图在直角坐标系中,A(-2,0),B(8,0),以AB为直径的半圆P与y轴交于点M,以AB为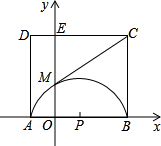 一边作正方形ABCD交y轴于E.
一边作正方形ABCD交y轴于E.
(1)写出AB边的长;
(2)连接CM,试说明直线CM是否与⊙P相切,说理理由;
(3)在x轴的正半轴上是否存在一点N,使得⊙N与⊙P、直线CP都相切?若存在,请求出点N的坐标;若不存在,请说明理由.
解:(1)8-(-2)=10;
(2)连接PC、PM,AM、BM,
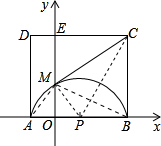
则∠AMB=90°(直径所对的圆周角等于90°),
故可得△AMO∽△MBO,
∵BC=10,PB=5,
∴CP2=BC2+PB2=125,
∵OA=2,OB=8,
∴OM2=OA•OB=16,
∴OM=4
∵EM=6,EC=8,
∴CM2=CE2+EM2=100;
∵CM2+MP2=PC2,
∴∠PMC=90°,
∴直线CM与OP相切;
(3)①当⊙N与直线CP相切,且与⊙P内切,在点P左边时;
设⊙N的半径为r1依题意知:
(CP-BC)2+r12=(5-r1)2;
又∵在Rt△PBC中,BC=10,PB=5,
∴PC=5
∴(5 -10)2=r12=(5-r2)2解得r1=10
-10)2=r12=(5-r2)2解得r1=10 -20,
-20,
∴ON1=28-10 ,
,
∴N(28-10 );
);
②当⊙N与直线CP内切且与⊙P内切,但在点P右边时;
根据对称此时满足条件的圆的半径r2=r1=10 -20>2
-20>2
∴ON2=10 -22,
-22,
∴N2(10 -22,0);
-22,0);
③当⊙N与直线CP相切且与⊙P外切时;
设⊙N的半径为r3,依题意得,
(10+5 )2+r32=(5+r3)2
)2+r32=(5+r3)2
解得r3=20+10
∴ON3=28+10 ,
,
∴N3(28+10 ,0).
,0).
分析:(1)易得正方形的边长等于点B的横坐标减去点A的横坐标.
(2)连接PC,PM,可利用勾股定理求得PC2长,CM2长,进而利用勾股定理可求得∠PMC=90°,那么是切线.
(3)注意分情况探讨内切,外切,点的不同位置等多种情况.
点评:连接圆心和切点是常用的辅助线方法;经过半径的外端并且与半径垂直的直线是圆的切线.
(2)连接PC、PM,AM、BM,

则∠AMB=90°(直径所对的圆周角等于90°),
故可得△AMO∽△MBO,
∵BC=10,PB=5,
∴CP2=BC2+PB2=125,
∵OA=2,OB=8,
∴OM2=OA•OB=16,
∴OM=4
∵EM=6,EC=8,
∴CM2=CE2+EM2=100;
∵CM2+MP2=PC2,
∴∠PMC=90°,
∴直线CM与OP相切;
(3)①当⊙N与直线CP相切,且与⊙P内切,在点P左边时;
设⊙N的半径为r1依题意知:
(CP-BC)2+r12=(5-r1)2;
又∵在Rt△PBC中,BC=10,PB=5,
∴PC=5

∴(5
 -10)2=r12=(5-r2)2解得r1=10
-10)2=r12=(5-r2)2解得r1=10 -20,
-20,∴ON1=28-10
 ,
,∴N(28-10
 );
);②当⊙N与直线CP内切且与⊙P内切,但在点P右边时;
根据对称此时满足条件的圆的半径r2=r1=10
 -20>2
-20>2∴ON2=10
 -22,
-22,∴N2(10
 -22,0);
-22,0);③当⊙N与直线CP相切且与⊙P外切时;
设⊙N的半径为r3,依题意得,
(10+5
 )2+r32=(5+r3)2
)2+r32=(5+r3)2解得r3=20+10

∴ON3=28+10
 ,
,∴N3(28+10
 ,0).
,0).分析:(1)易得正方形的边长等于点B的横坐标减去点A的横坐标.
(2)连接PC,PM,可利用勾股定理求得PC2长,CM2长,进而利用勾股定理可求得∠PMC=90°,那么是切线.
(3)注意分情况探讨内切,外切,点的不同位置等多种情况.
点评:连接圆心和切点是常用的辅助线方法;经过半径的外端并且与半径垂直的直线是圆的切线.

练习册系列答案
相关题目
 24、(北师大版)如图在直角坐标系中,右边的图案是由左边的图案经过平移以后得到的.左图案中左右眼睛的坐标分别是(-4,2)、(-2,2),右图中左眼的坐标是(3,4),则右图案中右眼的坐标是
24、(北师大版)如图在直角坐标系中,右边的图案是由左边的图案经过平移以后得到的.左图案中左右眼睛的坐标分别是(-4,2)、(-2,2),右图中左眼的坐标是(3,4),则右图案中右眼的坐标是
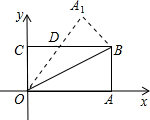 如图在直角坐标系中,将矩形OABC沿OB对折,使点A落在点A1处,OA=8,OC=4,则△BDO的面积为
如图在直角坐标系中,将矩形OABC沿OB对折,使点A落在点A1处,OA=8,OC=4,则△BDO的面积为
 如图在直角坐标系中,△AOB是等边三角形,若B点的坐标是(2,0),则A点的坐标是( )
如图在直角坐标系中,△AOB是等边三角形,若B点的坐标是(2,0),则A点的坐标是( )