题目内容
3.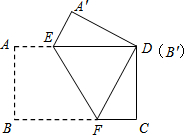 把一张长方形纸片按如图方式折叠,使顶点B和点D重合,折痕为EF.若AB=4cm,BC=8cm,则EF=( )
把一张长方形纸片按如图方式折叠,使顶点B和点D重合,折痕为EF.若AB=4cm,BC=8cm,则EF=( )| A. | 4cm | B. | 5cm | C. | 2$\sqrt{5}$cm | D. | 6cm |
分析 先证明∠DEF=∠EFD,从而得到ED=DF,然后利用翻折的性质得到FB=DF,设FB=DF=x,则FC=8-x,接下来在Rt△DFC中利用勾股定理列方程求解,从而得到FD=5,FC=3,故此ED=5,从而得到FG=2,然后再△EGF中利用勾股定理求得EF的长即可.
解答 解:过点E作EG⊥BC,垂足为G.
∵AD∥BC,
∴∠DEF=∠BFE.
由翻折的性质可知;∠BFE=∠DFE,BF=DF.
∴∠DEF=∠DFE.
∴DE=DF.
∴BF=DF=ED.
设BF=DF=ED=x,则FC=8-x.
Rt△DFC中,由勾股定理得;DF2=FC2+DC2,即x2=(8-x)2+42,
解得;x=5.
∴DE=5,FC=8-5=3.
∵DE=GC,
∴GC=5.
∴GF=2.
在Rt△EFG中,由勾股定理得:EF=$\sqrt{E{G}^{2}+F{G}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$.
故选:C.
点评 本题主要考查的是翻折的性质、勾股定理的应用、等腰三角形的判定,证得DE=DF是解题的关键.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
14.关于两点之间的距离,下列说法中不正确的是( )
| A. | 连接两点的线段就是两点之间的距离 | |
| B. | 如果线段AB=AC,那么点A与点B的距离等于点A与点C的距离 | |
| C. | 连接两点的线段的长度,是两点间的距离 | |
| D. | 两点之间的距离是连接两点的所有线的长度中,长度最短的 |
18.某同学做了一道数学题:已知两个多项式A、B,计算2A+B,他误将“2A+B”看成“A+2B”,求得的结果是9x2-2x+7,已知B=x2+3x-2,则2A+B的正确答案为15x2-13x+20.
8. 如图,在数轴上点P的位置被一滴墨水遮挡了,那么请估计数轴上点P表示的数可能是( )
如图,在数轴上点P的位置被一滴墨水遮挡了,那么请估计数轴上点P表示的数可能是( )
 如图,在数轴上点P的位置被一滴墨水遮挡了,那么请估计数轴上点P表示的数可能是( )
如图,在数轴上点P的位置被一滴墨水遮挡了,那么请估计数轴上点P表示的数可能是( )| A. | -2.6 | B. | -1.4 | C. | 2.6 | D. | 1.4 |
 如图是某时刻在镜子中看到准确时钟的情况,则实际时间是7点20分(或7:20).
如图是某时刻在镜子中看到准确时钟的情况,则实际时间是7点20分(或7:20). =0,
=0, =4,
=4, =-7,按此规律,计算
=-7,按此规律,计算 =18.
=18.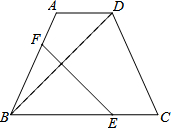 如图,在等腰梯形ABCD中,AD∥BC,∠ADB=45°,翻折梯形ABCD,使点B与点D重合,折痕分别交边AB、BC于点F、E,若AD=6,BC=14,那么cot∠C=$\frac{2}{5}$.
如图,在等腰梯形ABCD中,AD∥BC,∠ADB=45°,翻折梯形ABCD,使点B与点D重合,折痕分别交边AB、BC于点F、E,若AD=6,BC=14,那么cot∠C=$\frac{2}{5}$.