题目内容
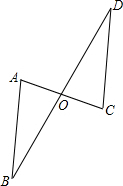如图，线段AC、BD相交于点O，且AO=2，AC=5，BO=10，OD=15，求证：∠A=∠C．
解：∵AO=2，AC=5，
∴OC=AC-AO=5-2=3，
∴
=
，
∵BO=10，OD=15，
∴
=
=，
∴==，
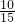∵∠AOB=∠COD，
∴△AOB∽△COD，
∴∠A=∠C．
分析：先根据AO=2，AC=5求出OC的长，由相似三角形的判定定理得出△AOB∽△COD，由相似三角形的对应角相等即可得出结论．
点评：本题考查的是相似三角形的判定与性质，根据题意得出△AOB∽△COD是解答此题的关键．
∴OC=AC-AO=5-2=3，
∴
=，∵BO=10，OD=15，
∴
==，∴
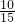==，∵∠AOB=∠COD，
∴△AOB∽△COD，
∴∠A=∠C．
分析：先根据AO=2，AC=5求出OC的长，由相似三角形的判定定理得出△AOB∽△COD，由相似三角形的对应角相等即可得出结论．
点评：本题考查的是相似三角形的判定与性质，根据题意得出△AOB∽△COD是解答此题的关键．
练习册系列答案
相关题目
如图，线段AC、BD相交于点O，且AB∥CD，AB=CD，此图形是中心对称图形吗？试说明你的理由．
如图，线段AC与BD相交于点O，且OA=OC，请添加一个条件，使△OAB≌△OCD，这个条件可以是（ ）
如图，线段AC、BD相交于点0，OA=OC，OB=OD，那么AB、CD的位置关系是