题目内容
20.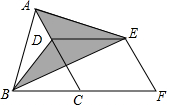 如图,已知△ABC的面积为24,点D在线段AC上,点F在线段BC的延长线上,且BF=2CF,四边形DCFE是平行四边形,则图中阴影部分的面积为( )
如图,已知△ABC的面积为24,点D在线段AC上,点F在线段BC的延长线上,且BF=2CF,四边形DCFE是平行四边形,则图中阴影部分的面积为( )| A. | 8 | B. | 12 | C. | 20 | D. | 24 |
分析 连接EC,过A作AM∥BC交FE的延长线于M,求出平行四边形ACFM,根据等底等高的三角形面积相等得出△BDE的面积和△CDE的面积相等,△ADE的面积和△AME的面积相等,推出阴影部分的面积等于平行四边形ACFM的面积的一半,即可求出答案.
解答 解:连接EC,过A作AM∥BC交FE的延长线于M,如图所示:
∵四边形CDEF是平行四边形,
∴DE∥CF,EF∥CD,
∴AM∥DE∥CF,AC∥FM,
∴四边形ACFM是平行四边形,
∵△BDE边DE上的高和△CDE的边DE上的高相同,
∴△BDE的面积和△CDE的面积相等,
同理:△ADE的面积和△AME的面积相等,
∴阴影部分的面积等于平行四边形ACFM的面积的一半,
∵△ABC的面积为24,
∴$\frac{1}{2}$BC×hBC=24,
∵BF=2CF,
∴BC=CF,
∵AM∥CF,
∴平行四边形ACFM的面积=BC×hBC=48,
∴阴影部分的面积=24,
故选D.
点评 本题考查了平行四边形的性质和判定,三角形的面积的计算,主要考查学生的推理能力和转化能力,题目比较好,但是有一定的难度.

练习册系列答案
相关题目
10.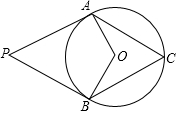 如图,PA、PB是⊙O的两条切线,A、B为切点,C为优弧BA上一动点.若OA=15,sin∠C=$\frac{4}{5}$,则S△PAB的值为( )
如图,PA、PB是⊙O的两条切线,A、B为切点,C为优弧BA上一动点.若OA=15,sin∠C=$\frac{4}{5}$,则S△PAB的值为( )
 如图,PA、PB是⊙O的两条切线,A、B为切点,C为优弧BA上一动点.若OA=15,sin∠C=$\frac{4}{5}$,则S△PAB的值为( )
如图,PA、PB是⊙O的两条切线,A、B为切点,C为优弧BA上一动点.若OA=15,sin∠C=$\frac{4}{5}$,则S△PAB的值为( )| A. | 108 | B. | 150 | C. | 300 | D. | 192 |
11.某校甲、乙两支仪仗队员的身高(单位;cm)如下:
你认为身高更整齐的队伍是甲队.
| 甲队 | 176 | 175 | 175 | 174 | 176 | 175 |
| 乙队 | 170 | 180 | 178 | 175 | 180 | 176 |
8.如果a=-3-2,b=-0.32,c=(-$\frac{1}{3}$)-2,d=(-$\frac{1}{5}$)0,那么a,b,c,d三数的大小为( )
| A. | a<b<c<d | B. | b<a<d<c | C. | a<d<c<b | D. | a<b<d<c |
15.据新华社北京2017年1月20日电国家统计局20日发布数据,初步核算,2016年我国国内生产总值(GDP)约74万亿元,若将74万亿用科学记数法表示为( )
| A. | 7.4×1013 | B. | 7.4×1012 | C. | 74×1013 | D. | 0.74×1012 |
5.已知:a=(-99)0,b=(-0.1)-1,c=(-$\frac{5}{3}$)-2,那么a,b,c三数的大小为( )
| A. | a<b<c | B. | b<a<c | C. | b<c<a | D. | a<c<b |
12.已知地球距离月球表面约为384000千米,那么这个距离用科学记数法(保留三个有效数字)表示应为( )
| A. | 3.84×104千米 | B. | 3.84×105千米 | C. | 3.84×106千米 | D. | 38.4×104千米 |
9. 如图,已知AB∥CD,则下列正确的是( )
如图,已知AB∥CD,则下列正确的是( )
 如图,已知AB∥CD,则下列正确的是( )
如图,已知AB∥CD,则下列正确的是( )| A. | ∠1=∠2 | B. | ∠1+∠3=∠2 | C. | ∠1+∠2=180° | D. | ∠1+∠3=180° |
10.下列各式的计算结果中,不正确的是( )
| A. | 2x2y-xy2-(x2y-3xy2)=x2y+2xy2 | B. | $\sqrt{20}$-$\sqrt{5}$=$\sqrt{15}$ | ||
| C. | (2a2)3=8a6 | D. | -a2•3a=-3a3 |