Question

17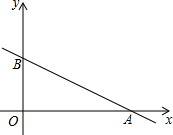．已知一次函数y=-$\frac{1}{2}$x+4的图象与x轴、y轴分别相交于点A、B，梯形AOBC的边AC=5，且OA∥BC．
（1）求点C的坐标；
（2）如果点A、C在一次函数y=kx+b（k、b为常数，且k＜0）的图象上，求这个一次函数的解析式．

Answer 1

分析 （1）根据梯形的对边平行，画出图形，结合勾股定理求解；
（2）根据（1）中所求C点坐标，一次函数y=kx+b中k＜0的条件，确定C的坐标，求一次函数解析式．

解答 解：（1）如图，

∵一次函数y=-$\frac{1}{2}$x+4的图象与x轴、y轴分别相交于点A、B，
∴A（8，0），B（0，4）．
在梯形AOBC中，OA=8，OB=4，
当BC∥OA时，设点C（x，4）．
∵AC=5，
∴（x-8）²+（4-0）²=5²，
∴x₁=5，x₂=11，
这时点C的坐标为（5，4）或（11，4），
∴点C的坐标为（5，4）或（11，4）；

（2）∵点A、C在一次函数y=kx+b（k＜0）的图象上，
∴点（8，5）与（11，4）都不符合题意，只有当C为（5，4）时，k＜0，
∴$\left\{\begin{array}{l}{8k+b=0}\\{5k+b=4}\end{array}\right.$，
∴$\left\{\begin{array}{l}{k=-\frac{4}{3}}\\{b=\frac{32}{3}}\end{array}\right.$，
∴这个一次函数的解析式为y=-$\frac{4}{3}$x+$\frac{32}{3}$．

点评 本题考查了一次函数的综合运用．根据组成梯形的字母顺序，梯形的底边，分类求C点坐标，再求一次函数解析式．