Question

△ABC中，∠A=70°，△ABC的角平分线BD，CE交于点O，则∠BOC=

 

度．

Answer 1

分析：根据三角形内角和定理和角平分线的定义解答．

解答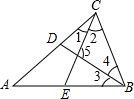：解：∵BD平分∠ABC，则∠4=

1

2

∠ABC，
CE平分∠ACB，则∠2=

1

2

∠ACB，
∴∠2+∠4=

1

2

（∠ABC+∠ACB）=

1

2

（180°-∠A）=

1

2

（180°-70°）=55°，
∴在△BOC中，∠BOC=180°-55°=125°．

点评：三角形的一个外角等于与它不相邻的两个内角的和．