题目内容
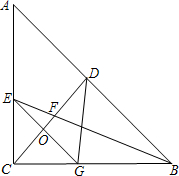 如图,Rt△ABC中,∠ACB=90°,AC=BC,点D是AB的中点,BE平分∠ABC,分别交AC、CD于点E、F,过点E作EG∥AB,分别交BC、CD于点G、O,连接DG.下列结论:
如图,Rt△ABC中,∠ACB=90°,AC=BC,点D是AB的中点,BE平分∠ABC,分别交AC、CD于点E、F,过点E作EG∥AB,分别交BC、CD于点G、O,连接DG.下列结论:
①EG=AE;②∠BGD=∠BDG;③S△ABE=2S△CBE;④DF= BG;⑤AC=(
BG;⑤AC=( +1)CF.
+1)CF.
其中正确结论的个数为
- A.2个
- B.3个
- C.4个
- D.5个
B
分析:过点E作EH⊥AB于H,根据角平分线上的点到角的两边的距离相等可得EH=EC,然后判断出△ABC、△AEH和△ECG都是等腰直角三角形,根据等腰直角三角形的性质可得AE= EH,EG=
EH,EG= EC,从而得到EG=AE,判断出①正确;根据等腰直角三角形的性质,BG=EG=
EC,从而得到EG=AE,判断出①正确;根据等腰直角三角形的性质,BG=EG= CG,BD=
CG,BD= (CG+
(CG+ CG),求出BG≠BD,所以∠BGD≠∠BDG,判断出②错误;AE=
CG),求出BG≠BD,所以∠BGD≠∠BDG,判断出②错误;AE= EH=
EH= CE,根据等高的三角形的面积的比等于底边的比求出S△ABE=
CE,根据等高的三角形的面积的比等于底边的比求出S△ABE= S△CBE,判断出③错误;求出△BDF和△BCE相似,根据相似三角形对应边成比例求出
S△CBE,判断出③错误;求出△BDF和△BCE相似,根据相似三角形对应边成比例求出 =
= =
= ,根据角平分线的定义求出∠CBE=22.5°,然后求出∠BEG=22.5°,从而得到∠CBE=∠BEG,根据等角对等边可得BG=EG,再根据EG=
,根据角平分线的定义求出∠CBE=22.5°,然后求出∠BEG=22.5°,从而得到∠CBE=∠BEG,根据等角对等边可得BG=EG,再根据EG= CE整理即可得到DF=
CE整理即可得到DF= BG,判断出④正确;根据等腰直角三角形的性质可得BC=
BG,判断出④正确;根据等腰直角三角形的性质可得BC= CD,再根据CF=CD-DF整理即可得解,判断出⑤正确.
CD,再根据CF=CD-DF整理即可得解,判断出⑤正确.
解答:如图,过点E作EH⊥AB于H,
∵BE平分∠ABC,
∴EH=EC,
∵∠ACB=90°,AC=BC,EG∥AB,
∴△ABC、△AEH和△ECG都是等腰直角三角形,
∴AE= EH,EG=
EH,EG= EC,
EC,
∴EG=AE,故①正确;
由等腰直角三角形的性质可得,BG=EG= CG,BD=
CG,BD= (CG+
(CG+ CG)=(
CG)=( +1)CG,
+1)CG,
∴BG≠BD,
∴∠BGD≠∠BDG,故②错误;
又∵AE= EH=
EH= CE,
CE,
∴S△ABE= S△CBE,故③错误;
S△CBE,故③错误;
∵BE平分∠ABC,
∴∠ABE=∠CBE=22.5°,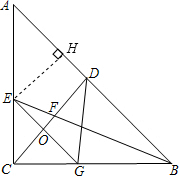
∵点D是AB的中点,
∴CD⊥AB,
∴∠BDF=∠ACB=90°,
∴△BDF∽△BCE,
∴ =
= =
= ,
,
又∵∠BEG=∠CGE-∠CBE=45°-22.5°=22.5°,
∴∠CBE=∠BEG,
∴BG=EG,
又∵EG= CE,
CE,
∴DF= CE=
CE= ×
× BG=
BG= BG,故④正确;
BG,故④正确;
由等腰直角三角形的性质可得,BC= CD,
CD,
CF=CD-DF= BC-
BC- BG,
BG,
∵CG= EG=
EG= BG,
BG,
∴BC= BG+BG,
BG+BG,
∴BG=(2- )BC,
)BC,
∴CF= BC-
BC- (2-
(2- )BC=(
)BC=( -1)BC,
-1)BC,
∴BC=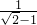 CF=(
CF=( +1)CF,
+1)CF,
∴AC=( +1)CF,故⑤正确.
+1)CF,故⑤正确.
综上所述,正确的有①④⑤共3个.
故选B.
点评:本题考查了相似三角形的判定与性质,等腰直角三角形的判定与性质,角平分线上的点到角的两边的距离相等的性质,等高的三角形的面积的比等于底边的比,熟练掌握各性质并准确识图是解题的关键,本题难点在于多次利用等腰直角三角形的性质.
分析:过点E作EH⊥AB于H,根据角平分线上的点到角的两边的距离相等可得EH=EC,然后判断出△ABC、△AEH和△ECG都是等腰直角三角形,根据等腰直角三角形的性质可得AE=
 EH,EG=
EH,EG= EC,从而得到EG=AE,判断出①正确;根据等腰直角三角形的性质,BG=EG=
EC,从而得到EG=AE,判断出①正确;根据等腰直角三角形的性质,BG=EG= CG,BD=
CG,BD= (CG+
(CG+ CG),求出BG≠BD,所以∠BGD≠∠BDG,判断出②错误;AE=
CG),求出BG≠BD,所以∠BGD≠∠BDG,判断出②错误;AE= EH=
EH= CE,根据等高的三角形的面积的比等于底边的比求出S△ABE=
CE,根据等高的三角形的面积的比等于底边的比求出S△ABE= S△CBE,判断出③错误;求出△BDF和△BCE相似,根据相似三角形对应边成比例求出
S△CBE,判断出③错误;求出△BDF和△BCE相似,根据相似三角形对应边成比例求出 =
= =
= ,根据角平分线的定义求出∠CBE=22.5°,然后求出∠BEG=22.5°,从而得到∠CBE=∠BEG,根据等角对等边可得BG=EG,再根据EG=
,根据角平分线的定义求出∠CBE=22.5°,然后求出∠BEG=22.5°,从而得到∠CBE=∠BEG,根据等角对等边可得BG=EG,再根据EG= CE整理即可得到DF=
CE整理即可得到DF= BG,判断出④正确;根据等腰直角三角形的性质可得BC=
BG,判断出④正确;根据等腰直角三角形的性质可得BC= CD,再根据CF=CD-DF整理即可得解,判断出⑤正确.
CD,再根据CF=CD-DF整理即可得解,判断出⑤正确.解答:如图,过点E作EH⊥AB于H,
∵BE平分∠ABC,
∴EH=EC,
∵∠ACB=90°,AC=BC,EG∥AB,
∴△ABC、△AEH和△ECG都是等腰直角三角形,
∴AE=
 EH,EG=
EH,EG= EC,
EC,∴EG=AE,故①正确;
由等腰直角三角形的性质可得,BG=EG=
 CG,BD=
CG,BD= (CG+
(CG+ CG)=(
CG)=( +1)CG,
+1)CG,∴BG≠BD,
∴∠BGD≠∠BDG,故②错误;
又∵AE=
 EH=
EH= CE,
CE,∴S△ABE=
 S△CBE,故③错误;
S△CBE,故③错误;∵BE平分∠ABC,
∴∠ABE=∠CBE=22.5°,

∵点D是AB的中点,
∴CD⊥AB,
∴∠BDF=∠ACB=90°,
∴△BDF∽△BCE,
∴
 =
= =
= ,
,又∵∠BEG=∠CGE-∠CBE=45°-22.5°=22.5°,
∴∠CBE=∠BEG,
∴BG=EG,
又∵EG=
 CE,
CE,∴DF=
 CE=
CE= ×
× BG=
BG= BG,故④正确;
BG,故④正确;由等腰直角三角形的性质可得,BC=
 CD,
CD,CF=CD-DF=
 BC-
BC- BG,
BG,∵CG=
 EG=
EG= BG,
BG,∴BC=
 BG+BG,
BG+BG,∴BG=(2-
 )BC,
)BC,∴CF=
 BC-
BC- (2-
(2- )BC=(
)BC=( -1)BC,
-1)BC,∴BC=
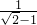 CF=(
CF=( +1)CF,
+1)CF,∴AC=(
 +1)CF,故⑤正确.
+1)CF,故⑤正确.综上所述,正确的有①④⑤共3个.
故选B.
点评:本题考查了相似三角形的判定与性质,等腰直角三角形的判定与性质,角平分线上的点到角的两边的距离相等的性质,等高的三角形的面积的比等于底边的比,熟练掌握各性质并准确识图是解题的关键,本题难点在于多次利用等腰直角三角形的性质.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目

 如图,Rt△ABC中,∠ACB=90°,tanB=
如图,Rt△ABC中,∠ACB=90°,tanB= 如图,Rt△ABC中,∠C=90°,BC=3,AC=4,若△ABC∽△BDC,则CD=( )
如图,Rt△ABC中,∠C=90°,BC=3,AC=4,若△ABC∽△BDC,则CD=( ) 如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F.
如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F. 如图,Rt△ABC中,∠ABC=90゜,BD⊥AC于D,∠CBD=α,AB=3,BC=4.
如图,Rt△ABC中,∠ABC=90゜,BD⊥AC于D,∠CBD=α,AB=3,BC=4.