题目内容
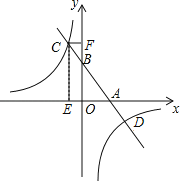
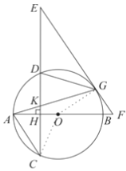
【题目】如图,![]() 是
是![]() 的直径,弦
的直径,弦![]() 于
于![]() ,
,![]() 为
为![]() 上一点,连接
上一点,连接![]() 交
交![]() 于
于![]() ,在
,在![]() 的延长线上取一点
的延长线上取一点![]() ,使
,使![]() ,
,![]() 的延长线交
的延长线交![]() 的延长线于
的延长线于![]() .
.
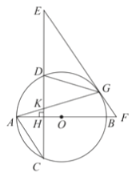
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)连接![]() ,若
,若![]() 时.
时.
①求证:![]() ;
;
②若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)①见解析,②![]()
【解析】
(1)连接OG,由EG=EK知∠KGE=∠GKE=∠AKH,结合OA=OG知∠OGA=∠OAG,根据CD⊥AB得∠AKH+∠OAG=90°,从而得出∠KGE+∠OGA=90°,据此即可得证;
(2)①由AC∥EF知∠E=∠C=∠AGD,结合∠DKG=∠CKE即可证得△KGD∽△KGE;
②连接OG,由![]() ,设
,设 ![]() 可得
可得![]() ,
,![]()
![]() 利用
利用 ![]() 得
得 ![]() 即可知 CH
即可知 CH![]()
![]() 再设
再设![]() 半径为R, 由
半径为R, 由 ![]() 可求得
可求得 ![]() 根据
根据 ![]() 知
知 ![]() 从而得出答案.
从而得出答案.
(1)如图,连接![]() .∵
.∵![]() ,
,
∴![]() ,
,
又![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() 是
是![]() 的切线.
的切线.
(2)①∵![]() ,∴
,∴![]() ,
,
又![]() ,∴
,∴![]() ,
,
又![]() ,
,
∴![]() .
.
②连接![]() ,如图所示.∵
,如图所示.∵![]() ,
,![]() ,
,
设![]() ,∴
,∴![]() ,
,![]() ,则
,则![]()
![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() .
.
在![]() 中,根据勾股定理得
中,根据勾股定理得![]() ,
,
即![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,
设![]() 半径为
半径为![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
由勾股定理得:![]() ,
,![]() ,∴
,∴![]()
在![]() 中,
中,![]() ,∴
,∴![]() ,
,
∴![]()

练习册系列答案
相关题目