Question

【题目】已知，在平面直角坐标系中，二次函数的图象与轴交于点，与轴交于点，点的坐标为，点的坐标为．

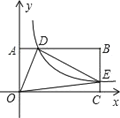
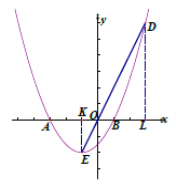
（1）如图1，分别求的值；

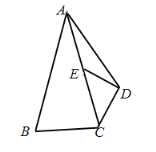
（2）如图2，点为第一象限的抛物线上一点，连接并延长交抛物线于点，，求点的坐标；

（3）在（2）的条件下，点为第一象限的抛物线上一点，过点作轴于点，连接、，点为第二象限的抛物线上一点，且点与点关于抛物线的对称轴对称，连接，设，，点为线段上一点，点为第三象限的抛物线上一点，分别连接，满足，，过点作的平行线，交轴于点，求直线的解析式．

Answer 1

【答案】（1），；（2）；（3）．

【解析】

（1）将点A、B的坐标代入抛物线表达式，即可求解；
（2）作轴于K，轴于L，OD=3OE，则OL=3OK，DL=3KE，设点E的横坐标为t，则点D的横坐标为-3t，则点E、D的坐标分别为：（t，）、（-3t，-+3t+），即可求解；

（3）设点的横坐标为，可得PH=m2+m-，过作EF∥y轴交于点交轴于点，TE=PH+YE=m2+m-+2=（m+1）2，tan∠AHE=，tan∠PET=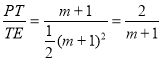，而∠AHE+∠EPH=2α，故∠AHE=∠PET=∠EPH=α，PH=PQtanα，即m2+m-=（2m+2）×，解得：m=2-1，故YH=m+1=2，PQ=4，点P、Q的坐标分别为：（2-1，4）、（-2-1，4），tan∠YHE=，tan∠PQH=；证明△PMH≌△WNH，则PH=WH，而QH=2PH，故QW=HW，即W是QH的中点，则W（-1，2），再根据待定系数法即可求解．

解：（1）把、分别代入得：

，解得；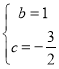

（2）如图2，由（1）得，作轴于K，轴于L，

∴EK∥DL，∴．

∵，∴，

设点的横坐标为，，，

∴的横坐标为，分别把和代入抛物线解析式得，

∴，

∴，．

∵，

∴，∴，

∴，

∴，

解得（舍），，

∴．

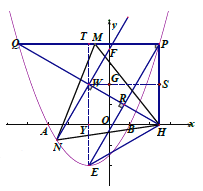
（3）如图3，设点的横坐标为，把代入抛物线得，

∴．

过作EF∥y轴交于点交轴于点，∴轴．

∵点与点关于抛物线的对称轴对称，∴PQ∥x轴，，

∴，点坐标为，

又∵轴，∴ET∥PH，∴，

∴，∴四边形为矩形，

∴，∴，

∴，，，

∴．

∴，，

∴，∴．

又∵，∴．

∵，

∴解得，

∵，∴．

∴，，

把代入抛物线得，∴，∴，

∴，∴，∴，

∴，∴．

若交于点，

∵NF∥PE，∴，∴，

∵，∴，

∴，，，

∴，∴，∴．

作WS∥PQ，交于点交轴于点，

∴△WSH∽△QPH，∴．

∵∴，

∴，，

∴．

∵，∴，∴．

设的解析式为，把、代入得，

解得，∴．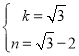

∵FN∥PE，∴设的解析式为，把代入得，

∴的解析式为．