Question

【题目】阅读下列材料：

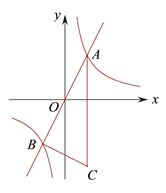
某同学遇到这样一个问题：在平面直角坐标系中，已知直线点在抛物线上，求点到直线的距离．

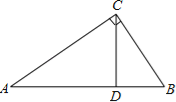
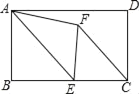
如图1，他过点作于点轴分别交轴于点交直线于点．他发现，可求出的长，再利用求出的长，即为点到直线的距离．

　　　　　

请回答：

（1）图1中， ，点到直线的距离 ．

参考该同学思考问题的方法，解决下列问题:

在平面直角坐标系中，点是抛物线上的一动点，设点到直线的距离为．

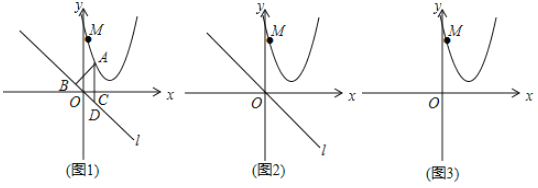
（2）如图2，

①，则点的坐标为 ；

②，在点运动的过程中，求的最小值；

（3）如图3，，在点运动的过程中，的最小值是 ．

Answer 1

【答案】（1）3，；（2）①（0，5）或（3，2）；②；（3）

【解析】

（1）由题意得：d=AB=AD=，即可求解；（2）如设点M的坐标为（m，m2-4m+5），则点N坐标为（m，-m），则由（1）知：d=MH=MN，即可求解；（3）如下图，点M的坐标为（m，m2-4m+5），则点N坐标为（m，2m-7），由题意得：tanα=2，则d=MH=MNcosα即可求解．

（1）∵点A（1，t）在抛物线y=x2-4x+5上，

∴t=1-4+5=2，

∴点A的坐标为（1，2）．

∵AD∥y轴交直线l于点D，直线l：y=-x，

∴点D的坐标为（1，-1），

∴AD=2-（-1）=3．

∵△ABD为等腰直角三角形，∠ABD=90°，

∴d=AB=AD=．

（2）如图，过点M作y轴的平行线交直线l于点N，过点M作MH⊥l，交l于点H，设点M的坐标为（m，m2-4m+5），则点N坐标为（m，-m），则MN=m2-3m+5，

，

∵，

∴，

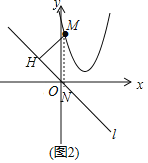解得：M坐标为（0，5）或（3，2）；

②，

则d的最小值；

（3）如图，过点M作y轴的平行线交x轴于点G，交直线l于点N，过点M作MH⊥l，交l于点H，

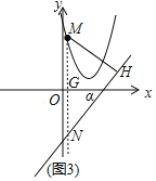
设点M的坐标为（m，m2-4m+5），则点N坐标为（m，2m-7），

由题意得：tanα=2，则，

则d=MH=MN（m2-4m+5-2m+7）= [（m-3）2+3]，

故d的最小值为．