Question

【题目】在四边形ABCD中，AD∥BC，BC⊥CD，AD=6cm，BC=10cm，点E从A出发以1cm/s的速度向D运动，点F从点B出发，以2cm/s的速度向点C运动，当其中一点到达终点，而另一点也随之停止，设运动时间为t.

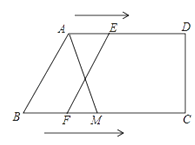
（1）t取何值时，四边形EFCD为矩形？

（2）M是BC上一点，且BM=4，t取何值时，以A、M、E、F为顶点的四边形是平行四边形？

Answer 1

【答案】（1）t＝4s；（2）t＝4s或s.

【解析】

（1）当DE＝CF时，四边形EFCD为矩形，列出方程即可解决问题；

（2）分两种情形列出方程即可解决问题；

解：（1）当DE＝CF时，四边形EFCD为矩形，

则有6t＝102t，解得t＝4，

答：t＝4s时，四边形EFCD为矩形；

（2）①当点F在线段BM上，AE＝FM时，以A、M、E、F为顶点的四边形是平行四边形，

则有t＝42t，解得t＝，

②当F在线段CM上，AE＝FM时，以A、M、E、F为顶点的四边形是平行四边形，

则有t＝2t4，解得t＝4，

综上所述，t＝4s或s时，以A、M、E、F为顶点的四边形是平行四边形．