题目内容
2.已知函数kx+(k-1)y=1(k为正整数)的图象与两坐标轴围成的面积为Sk(k=1,2,3,…,2000,)求S1+S2+…+S2000的值.分析 令x=0,y=0,分别求出图象与坐标轴的交点,再根据三角形面积公式表示S1,S2,S3,…S2000,根据规律求和.
解答 解:令x=0,得y=$\frac{1}{k-1}$,y=0,得x=$\frac{1}{k}$,
∴S=$\frac{1}{2}$×$\frac{1}{k-1}$×$\frac{1}{k}$=$\frac{1}{2}$($\frac{1}{k-1}$-$\frac{1}{k}$),
∴S1+S2+…+S2000=0+$\frac{1}{2}$(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{1999}$-$\frac{1}{2000}$)
=$\frac{1999}{4000}$.
点评 本题考查了一次函数的综合运用.关键是由函数关系式求直线与坐标轴的交点坐标,得出三角形面积的一般关系式,寻找抵消规律.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4. 如图,直线y=kx+b过点A(0,3)和点B(-4,0),则方程kx+b=0的解是( )
如图,直线y=kx+b过点A(0,3)和点B(-4,0),则方程kx+b=0的解是( )
 如图,直线y=kx+b过点A(0,3)和点B(-4,0),则方程kx+b=0的解是( )
如图,直线y=kx+b过点A(0,3)和点B(-4,0),则方程kx+b=0的解是( )| A. | x=3 | B. | x=-3 | C. | x=4 | D. | x=-4 |
7.下列命题的逆命题不成立的是( )
| A. | 两直线平行,同位角相等 | B. | 两直线平行,同旁内角互补 | ||
| C. | 等腰三角形的底角相等 | D. | 对顶角相等 |
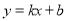 (
(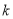 、
、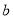 为常数,
为常数, 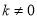 )图象如图所示,则关于
)图象如图所示,则关于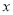 的不等式
的不等式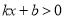 的解集为( )
的解集为( )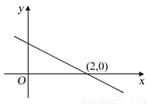
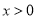 B.
B. 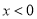 C.
C. 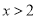 D.
D. 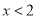
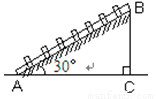
 如图,O是菱形ABCD一条对角线BD上的一个点,它是菱形一边AB的距离(OE)是2cm,那么O到BC的距离是多少?
如图,O是菱形ABCD一条对角线BD上的一个点,它是菱形一边AB的距离(OE)是2cm,那么O到BC的距离是多少?