题目内容
【题目】已知:点![]() 为直线
为直线![]() 上一点,
上一点,![]() ,射线
,射线![]() 平分
平分![]() ,设
,设![]() .
.
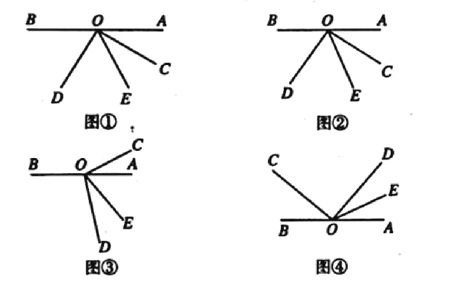
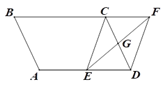
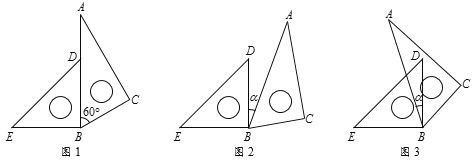
(1)如图①所示,若![]() ,则
,则![]() .
.
(2)若将![]() 绕点
绕点![]() 旋转至图②的位置,试用含
旋转至图②的位置,试用含![]() 的代数式表示
的代数式表示![]() 的大小,并说明理由;
的大小,并说明理由;
(3)若将![]() 绕点
绕点![]() 旋转至图③的位置,则用含
旋转至图③的位置,则用含![]() 的代数式表示
的代数式表示![]() 的大小,即
的大小,即![]() .
.
(4)若将![]() 绕点
绕点![]() 旋转至图④的位置,继续探究
旋转至图④的位置,继续探究![]() 和
和![]() 的数量关系,则用含
的数量关系,则用含![]() 的代数式表示
的代数式表示![]() 的大小,即
的大小,即![]() .
.
【答案】(1)50;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]()
【解析】
(1)根据“∠COD=90°,∠COE=25°”求出∠DOE的度数,再结合角平分线求出∠AOD的度数,即可得出答案;
(2)重复(1)中步骤,将∠COE的度数代替成![]() 计算即可得出答案;
计算即可得出答案;
(3)根据图得出∠DOE=∠COD-∠COE=90°-![]() ,结合角平分线的性质以及平角的性质计算即可得出答案;
,结合角平分线的性质以及平角的性质计算即可得出答案;
(4)根据图得出∠DOE=∠COE-∠COD=![]() -90°,结合角平分线的性质以及平角的性质计算即可得出答案.
-90°,结合角平分线的性质以及平角的性质计算即可得出答案.
解:(1)∵∠COD=90°,∠COE=25°
∴∠DOE=∠COD-∠COE=65°
又OE平分∠AOD
∴∠AOD=2∠DOE=130°
∴∠BOD=180°-∠AOD=50°
(2)∵∠COD=90°,∠COE=![]()
∴∠DOE=∠COD-∠COE=90°-![]()
又OE平分∠AOD
∴∠AOD=2∠DOE=180°-![]()
∴∠BOD=180°-∠AOD=2![]()
(3)∵∠COD=90°,∠COE=![]()
∴∠DOE=∠COD-∠COE=90°-![]()
又OE平分∠AOD
∴∠AOD=2∠DOE=180°-![]()
∴∠BOD=180°-∠AOD=2![]()
(4)∵∠COD=90°,∠COE=![]()
∴∠DOE=∠COE-∠COD=![]() -90°
-90°
又OE平分∠AOD
∴∠AOD=2∠DOE=![]() -180°
-180°
∴∠BOD=180°-∠AOD=360°-2![]()

【题目】垫球是排球运动的一项重要技术.下列图表中的数据分别是甲、乙、内三个运动员十次垫球测试的成绩,规则为每次测试连续垫球10个,每垫球到位1个记1分.
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
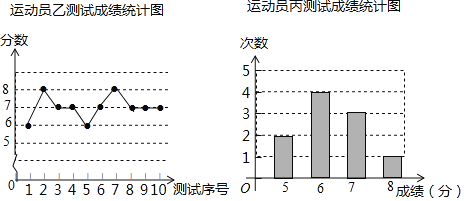
(1)写出运动员甲测试成绩的众数和中位数;
(2)试从平均数和方差两个角度综合分析,若在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?(参考数据:三人成绩的方差分别为S甲2=0.8、S乙2=0.4、s丙2=0.81)
【题目】某市雾霾天气趋于严重,甲商场根据民众健康需要,代理销售每台进价分别为600元、560
元的 A、B 两种型号的空气净化器,如表是近两周的销售情况:(进价、售价均保持不变,利润=销
售收入进货成本)
销售时段 | 销售数量 | 销售收入 (元) | |
A种型号 (台) | B种型号 (台) | ||
第一周 | 3 | 2 | 3960 |
第二周 | 5 | 4 | 7120 |
(1)求 A,B 两种型号的空气净化器的销售单价;
(2)该商店计划一次购进两种型号的空气净化器共30台,其中B型净化器的进货量不超过A型的2倍.设购进A型空气净化器为x台,这30台空气净化器的销售总利润为y元.
①请写出y关于x的函数关系式;
②该商店购进A型、B型净化器各多少台,才能使销售总利润最大?