题目内容
【题目】
是线段
上任一点，
，
两点分别从
同时向
点运动，且
点的运动速度为
，
点的运动速度为
，运动的时间为
.
（1）若
，
①运动
后，求
的长；
②当在线段
上运动时，试说明
；
（2）如果
时，
，试探索
的值.
【答案】（1）①3cm；②见解析；（2）
或11cm.
【解析】
（1）①先求出PB、CP与DB的长度，然后利用CD=CP+PB-DP即可求出答案；②用t表示出AC、DP、CD的长度即可求证AC=2CD；
（2）t=2时，求出CP、DB的长度，由于没有说明点D再C点的左边还是右边，故需要分情况讨论.
解：（1）①由题意可知：
，
∵
，∴
，
∴
；
②∵
，∴
，
∴
，∴
，
∴
；
（2）当
时，
，
当点
在
的右边时，如图所示：由于
，∴
，∴
，
∴
，
当点在的左边时，如图所示：∴
，∴
，
综上所述，或11cm.
【题目】某校数学兴趣小组根据学习函数的经验，对函数y＝
|x|+1的图象和性质进行了探究，探究过程如下：（1）自变量x的取值范围是全体实数，x与y的几组对应值如表：
X | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
Y | … | 3 | 2.5 | m | 1.5 | 1 | 1.5 | 2 | 2.5 | 3 | … |
（1）其中m＝ ．
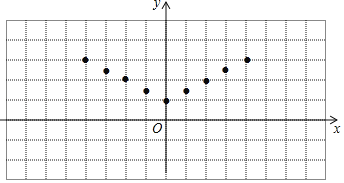
（2）如图，在平面直角坐标系xOy中，描出了上表中各对对应值为坐标的点，根据描出的点，画出该函数的图象；
（3）当2＜y≤3时，x的取值范围为 ．
【题目】在一个不透明的口袋里装有仅颜色不同的黑、白两种颜色的球20只，某学习小组做摸球实验．将球搅匀后从中随机摸出一个球，记下颜色，再把它放回袋中，不断重复，下表是活动进行中记下的一组数据
摸球的次数 | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数 | 58 | 96 | 116 | 295 | 484 | 601 |
摸到白球的频率 | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
（1）请你估计，当n很大时，摸到白球的频率将会接近 （精确到0.1）．
（2）假如你去摸一次，你摸到白球的概率是 ，摸到黑球的概率是 ．
（3）试估算口袋中黑、白两种颜色的球有多少只．
