题目内容
 如图,已知Rt△ABC中,∠ACB=90°,AC=3,BC=4,以AB、BC、AC为直径作半圆为成两月形,则阴影部分的面积为________.
如图,已知Rt△ABC中,∠ACB=90°,AC=3,BC=4,以AB、BC、AC为直径作半圆为成两月形,则阴影部分的面积为________.
6
分析:阴影部分面积可以看成是以AC、BC为直径的两个半圆的面积加上一个直角三角形ABC的面积减去一个以AB为直径的半圆的面积.
解答:∵∠ACB=90°,
∴AB2=AC2+CB2,
S阴影=直径为AC的半圆的面积+直径为BC的半圆的面积+S△ABC-直径为AB的半圆的面积,
= ×π×
×π× +
+ ×π×
×π× +
+ ×AC×CB-
×AC×CB- ×π×
×π×
= π(AC2+BC2-AB2)+
π(AC2+BC2-AB2)+ AC×BC
AC×BC
= ×3×4
×3×4
=6.
故答案为:6.
点评:此题主要考查了勾股定理,圆的面积计算以及三角形的面积计算,关键是找出阴影部分的面积是由哪几个规则图形的面积的和或差表示.
分析:阴影部分面积可以看成是以AC、BC为直径的两个半圆的面积加上一个直角三角形ABC的面积减去一个以AB为直径的半圆的面积.
解答:∵∠ACB=90°,
∴AB2=AC2+CB2,
S阴影=直径为AC的半圆的面积+直径为BC的半圆的面积+S△ABC-直径为AB的半圆的面积,
=
 ×π×
×π× +
+ ×π×
×π× +
+ ×AC×CB-
×AC×CB- ×π×
×π×
=
 π(AC2+BC2-AB2)+
π(AC2+BC2-AB2)+ AC×BC
AC×BC=
 ×3×4
×3×4=6.
故答案为:6.
点评:此题主要考查了勾股定理,圆的面积计算以及三角形的面积计算,关键是找出阴影部分的面积是由哪几个规则图形的面积的和或差表示.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 22、如图,已知Rt△ABC,AB=AC,∠ABC的平分线BD交AC于点D,BD的垂直平分线分别交AB,BC于点E、F,CD=CG.
22、如图,已知Rt△ABC,AB=AC,∠ABC的平分线BD交AC于点D,BD的垂直平分线分别交AB,BC于点E、F,CD=CG.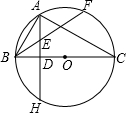 E,交⊙O于点F,且AE=BE.
E,交⊙O于点F,且AE=BE.
 5、如图,已知Rt△ABC中,∠BAC=90°,AB=AC,P是BC延长线上一点,PE⊥AB交BA延长线于E,PF⊥AC交AC延长线于F,D为BC中点,连接DE,DF.求证:DE=DF.
5、如图,已知Rt△ABC中,∠BAC=90°,AB=AC,P是BC延长线上一点,PE⊥AB交BA延长线于E,PF⊥AC交AC延长线于F,D为BC中点,连接DE,DF.求证:DE=DF. 如图,已知Rt△ABC中,∠CAB=30°,BC=5.过点A做AE⊥AB,且AE=15,连接BE交AC于点P.
如图,已知Rt△ABC中,∠CAB=30°,BC=5.过点A做AE⊥AB,且AE=15,连接BE交AC于点P. 如图,已知Rt△ABC中∠A=90°,AB=3,AC=4.将其沿边AB向右平移2个单位得到△FGE,则四边形ACEG的面积为
如图,已知Rt△ABC中∠A=90°,AB=3,AC=4.将其沿边AB向右平移2个单位得到△FGE,则四边形ACEG的面积为