Question

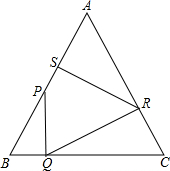
如图：等边三角形ABC的边长为1，P为AB边上的一个动点（不包括A、B），过P作PQ⊥BC于Q，过Q作QR⊥AC于R，再过R作RS⊥AB于S．设AP=x，AS=y．
（1）求y与x之间的函数关系式，并写出自变量取值范围；
（2）若SP=

1

4

，求AP的长；
（3）若S、P重合点为T，试说明当P、S不重合时，P、S中的哪一个更接近T点？将上述操作，即按逆时针方向，过垂足作相邻边的垂线，若操作不断进行，试依据你的结论，猜想无论P的初始位置如何，P、S…等这些点最终将会出现怎样的趋势？（只要直接写出结果）

Answer 1

分析：（1）本题可先在直角三角形PBQ中，用x表示出BQ的长，然后在直角三角形ASR中用y表示出AR的长，进而在直角三角形QRC中用y表示出QC的长，然后根据BQ+QC=1来得出y，x的函数关系式．
（2）SP的长实际就是y-x或x-y的值，可联立（1）的函数关系式即可分别得出x即AP的长．
（3）点S应该更接近T点，点S将更接近点T，猜想无论P的初始位置如何，P、S…这些点最终将会无限接近于点T．点T是AB边上的一个三等分点，靠近点A的那一个，当AP=

1

3

，AB=1，那么BP=

2

3

，BQ=

1

3

，QC=

2

3

，CR=

1

3

，AR=

2

3

，AS=

1

3

．即S，P重合．

解答：解：（1）在直角三角形PBQ中，∠B=60°，BP=1-x，
∴BQ=

1

2

（1-x）；
在直角三角形ASR中，∠A=60°，AS=y，
∴AR=2y；
在直角三角形CQR中，∠C=60°，RC=1-AR=1-2y，
∴CQ=2-4y
∵BC=1
∴

1

2

（1-x）+2-4y=1，即y=-

1

8

x+

3

8

（0＜x＜1）

（2）当S在P下方，
∵SP=

1

4

，即y-x=

1

4

∴x+

1

4

=-

1

8

x+

3

8

，解得x=

1

9

即AP=

1

9

．
当S在P上方，
∵SP=

1

4

，即x-y=

1

4

，
∴x-

1

4

=-

1

8

x+

3

8

，解得x=

5

9

即AP=

5

9

．


（3）S更加接近T．

点评：本题主要考查了等边三角形和直角三角形的性质以及定点、定值问题．在涉及定点和定值的问题中一般都有变量或动点，但最终的数值或点却是一定的．解决这类问题，一般都可采用特殊值或特殊的位置，探得定值或定点，如果需要的话再考虑证明．