题目内容
13．
如图，在△ABC中，点D，E分别在AB，AC上，若$\frac{AD}{DB}$=$\frac{AE}{EC}$，且AE=2，EC=4，DB=5，求AB的长．
分析 根据已知条件可证明△ADE∽△ABC，利用相似三角形的性质即可得到结论．
解答 解：∵AD：DB=AE：EC
∠A=∠A，
∴△ADE∽△ABC，
∴$\frac{AD}{DB}$=$\frac{AE}{EC}$，
∵AE=2，EC=4，DB=5，
∴AD=$\frac{5}{2}$，
∴AB=AD+DB=$\frac{15}{2}$．
点评 本题考查了相似三角形的判定和性质，熟练掌握相似三角形的判定和性质是解题的关键．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
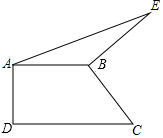如图，在四边形ABCD中，AB⊥AD，CD⊥AD，将BC按逆时针方向绕点B旋转90°，得到线段BE，连接AE．若AB=2，DC=4，则△ABE的面积为2．
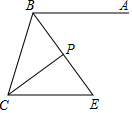已知：如图AB∥CE，BE平分∠ABC，CP平分∠BCE交BE于点P．