题目内容
如图①,P是△ABC边AC上的动点,以P为顶点作矩形PDEF,顶点D,E在边BC上,顶点F在边AB上;△ABC的底边BC及BC上的高的长分别为a , h,且是关于x的一元二次方程 的两个实数根,设过D, E,F三点的⊙O的面积为
的两个实数根,设过D, E,F三点的⊙O的面积为 ,矩形PDEF的面积为
,矩形PDEF的面积为

(1)求证:以a+h为边长的正方形面积与以a、h为边长的矩形面积之比不小于4;
(2)求
 的最小值;
的最小值;(3)当
 的值最小时,过点A作BC的平行线交直线BP与Q,这时线段AQ的长与m , n , k的取值是否有关?请说明理由。(11分)
的值最小时,过点A作BC的平行线交直线BP与Q,这时线段AQ的长与m , n , k的取值是否有关?请说明理由。(11分)
(1)略
(2)

(3)线段AQ的长与m,n,k的取值有关解析:
解:解法一:
(1)据题意,∵a+h=
 .
.∴所求正方形与矩形的面积之比:

 1分
1分 由
由 知
知 同号,
同号,  2分
2分(说明:此处未得出
 只扣1分, 不再影响下面评分)
只扣1分, 不再影响下面评分) 3分
3分即正方形与矩形的面积之比不小于4.
(2)∵∠FED=90º,∴DF为⊙O的直径.
|
 . 4分矩形PDEF的面积:
. 4分矩形PDEF的面积: .
.
|
 设
设
|

|

 ,
, 
|
 ,即
,即 时(EF=DE),
时(EF=DE),  的最小值为
的最小值为 7分
7分
|
 的值最小时,这时矩形PDEF的四边相等为正方形.过B点过BM⊥AQ,M为垂足,BM交直线PF于N点,设FP= e,
的值最小时,这时矩形PDEF的四边相等为正方形.过B点过BM⊥AQ,M为垂足,BM交直线PF于N点,设FP= e,
∵BN∥FE,NF∥BE,∴BN=EF,∴BN ="FP" =e.
由BC∥MQ,得:BM ="AG" =h.
∵AQ∥BC, PF∥BC, ∴AQ∥FP,
∴△FBP∽△ABQ. 8分 (说明:此处有多种相似关系可用,要同等分步骤评分)
∴
 ,……9分
,……9分∴
 .∴
.∴ ……10分
……10分 ……11分
……11分∴线段AQ的长与m,n,k的取值有关. (解题过程叙述基本清楚即可)
解法二:
(1)∵a,h为线段长,即a,h都大于0,
∴ah>0…………1分(说明:此处未得出
 只扣1分,再不影响下面评分)
只扣1分,再不影响下面评分)∵(a-h)2≥0,当a=h时等号成立.
故,(a-h)2=(a+h)2-4a h≥0. 2分
∴(a+h)2≥4a h,
∴
 ≥4.(﹡) 3分
≥4.(﹡) 3分这就证得
 ≥4.(叙述基本明晰即可)
≥4.(叙述基本明晰即可)(2)设矩形PDEF的边PD=x,DE=y,则⊙O的直径为
 .
.S⊙O=
 …………4分, S矩形PDEF=xy
…………4分, S矩形PDEF=xy
|
 =
=  =
= 6分
6分 由(1)(*), .
由(1)(*), . .
.
|
 的最小值是
的最小值是 7分
7分
|
 的值最小时,这时矩形PDEF的四边相等为正方形. ∴EF=PF.作AG⊥BC,G为垂足.
的值最小时,这时矩形PDEF的四边相等为正方形. ∴EF=PF.作AG⊥BC,G为垂足.
∵△AGB∽△FEB,∴
 .……8分
.……8分∵△AQB∽△FPB,
 ,……9分
,……9分∴
 =
= .
.而 EF=PF,∴AG="AQ=h," ……………10分
∴AG=h=
 ,
,或者AG=h=
 11分
11分∴线段AQ的长与m,n,k的取值有关. (解题过程叙述基本清楚即可)

练习册系列答案
相关题目
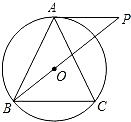 如图,圆O是△ABC的外接圆,AB=AC,过点A作AP∥BC,交BO的延长线于点P.
如图,圆O是△ABC的外接圆,AB=AC,过点A作AP∥BC,交BO的延长线于点P.
 (2012•利川市二模)如图,点P是△ABC三条角平分线的交点,若∠BPC=108°,则下列结论中正确的是( )
(2012•利川市二模)如图,点P是△ABC三条角平分线的交点,若∠BPC=108°,则下列结论中正确的是( ) 如图,点O是△ABC的内心,若∠BAC=86°,则∠BOC=( )
如图,点O是△ABC的内心,若∠BAC=86°,则∠BOC=( )