Question

如图所示，四边形ABCD是菱形，对角线AC，BD相交于点O，DH⊥AB于点H，连接OH，求证：∠DHO=∠DCO.

Answer 1

分析:根据菱形的性质可得点O是BD的中点，由直角三角形斜边上的中线等于斜边的一半，可得OH=OB，从而有△OHB是等腰三角形，所以∠OHB=∠OBH=∠ODC.由等角的余角相等即可证出∠DHO=∠DCO.

证明:∵ 四边形ABCD是菱形，

∴ OD=OB,∠COD=90°,∠ODC=∠OBH.

∵ DH⊥AB于点H，∴ ∠DHB=90°.

∴ HO=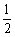BD=OB,∴ ∠OHB=∠OBH.

∴ ∠OHB=∠ODC.

在Rt△COD中，∠ODC+∠DCO=90°.

在Rt△DHB中，∠DHO+∠OHB=90°.

∴ ∠DHO=∠DCO.

点拨:本题综合考查了菱形的性质、直角三角形的性质及等腰三角形的性质.菱形的对角线互相垂直平分为充分利用直角三角形的性质创造了条件.