题目内容
（1）观察下列各式，你会发现什么规律？
3×5=15，而15=42-1，
5×7=35，而35=62-1，
| 第一行 | 1 |
| 第二行 |   |
| 第三行 |    |
| 第四行 |     |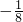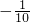
| 第五行 | -    |
| … | … |
…
11×13=143，而143=122-1
将你猜想到的规律用只含一个字母的式子表示出来______．
（2）将1，，，，，…按一定规律排成下表：
从表中可以看到第4行中，自左向右第3个数是，第5行中从左向右第2数是
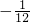，那么第199行中自左向右第8个数是______，第1998行中自左向第11个数是______．
解：（1）（2n+1）（2n+3）=（2n+2-1）（2n+2+1）=（2n+2）2-1．
（2）第199行的第一个数的分母是1+2+3+…+198+1=
+1=19702，
则第8个数的分母是19702+7=19709．
第1998行的第一个数的分母是
+1=1995004，
则第11个数的分母是1995004+10=1995014，则该数是-
．
故答案为：（2n+1）（2n+3）=（2n+2）2-1；
，-．
分析：（1）可设等号左边第一个因数为2n+1，那么第二个因数为2n+3，则等号右边为（2n+2）2-1；
（2）此题我们可以看出第几行就有几个数，且分母是偶数的数是负数．则199行的第一个数的分母是
1+2+3+…+198+1=+1=19702；第1998行的第一个数的分母是+1=1995004．
点评：本题考查了规律型：数字的变化．解决此类探究性问题，关键在观察、分析已知数据，寻找它们之间的相互联系，探寻其规律．第（1）题关键规律是分别找到等号左右两边的规律．第（2）题注意从符号的规律以及分母的规律去分析．
（2）第199行的第一个数的分母是1+2+3+…+198+1=
+1=19702，则第8个数的分母是19702+7=19709．
第1998行的第一个数的分母是
+1=1995004，则第11个数的分母是1995004+10=1995014，则该数是-
．故答案为：（2n+1）（2n+3）=（2n+2）2-1；
，-．分析：（1）可设等号左边第一个因数为2n+1，那么第二个因数为2n+3，则等号右边为（2n+2）2-1；
（2）此题我们可以看出第几行就有几个数，且分母是偶数的数是负数．则199行的第一个数的分母是
1+2+3+…+198+1=
+1=19702；第1998行的第一个数的分母是+1=1995004．点评：本题考查了规律型：数字的变化．解决此类探究性问题，关键在观察、分析已知数据，寻找它们之间的相互联系，探寻其规律．第（1）题关键规律是分别找到等号左右两边的规律．第（2）题注意从符号的规律以及分母的规律去分析．
练习册系列答案
阅读快车系列答案
相关题目
