题目内容
四边形ABCD∽四边形A′B′C′D′，∠A=70°，∠B′=108°，∠C′=92′，则∠D= 度．
【答案】分析：根据相似多边形的对应角相等可得．
解答：解：四边形ABCD∽四边形A′B′C′D′，
则∠B=∠B′=108°，∠C=∠C′=92′
四边形ABCD的内角和是360°，
因而∠D=360°-70°-108°-92°=90°．
点评：本题主要考查对相似多边形的性质，对应角相等这一性质的记忆．
解答：解：四边形ABCD∽四边形A′B′C′D′，
则∠B=∠B′=108°，∠C=∠C′=92′
四边形ABCD的内角和是360°，
因而∠D=360°-70°-108°-92°=90°．
点评：本题主要考查对相似多边形的性质，对应角相等这一性质的记忆．
练习册系列答案
名校课堂系列答案
相关题目
（2013•泉州）如图，顺次连结四边形ABCD四边的中点E、F、G、H，则四边形EFGH的形状一定是
如图，已知点M，N，P，Q分别是凸四边形ABCD四边的中点，在下列4个命题中：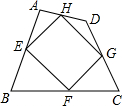
如图，已知E、F、G、H是四边形ABCD四边的中点，则四边形EFGH的形状为