题目内容
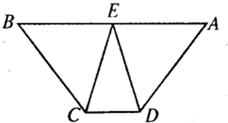21、如图，E是等腰梯形ABCD底边AB上的中点，求证：DE=CE．分析：根据等腰梯形的性质，可知CB=AD，∠CBE=∠DAE，又因为BE=AE，所以△CBE≌△DAE，则DE=CE．
解答：证明：∵等腰梯形ABCD，
∴BC=AD，∠CBE=∠DAE．
∵E是AB上的中点，
∴BE=AE．
∴△CBE≌△DAE（SAS）．
∴DE=CE．
∴BC=AD，∠CBE=∠DAE．
∵E是AB上的中点，
∴BE=AE．
∴△CBE≌△DAE（SAS）．
∴DE=CE．
点评：本题主要考查等腰梯形的性质的应用．
练习册系列答案
阅读快车系列答案
相关题目
13、如图，P是等腰梯形ABCD上底AD上一点，若∠A=∠BPC，则图中与△ABP相似的所有三角形是
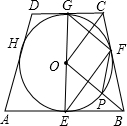如图，⊙O是等腰梯形ABCD的内切圆，切点分别为E，F，G，H，其中AB∥CD，连接OB交⊙O于点P，连接OC，OG，OE，FG，FP，下列结论：①EG为⊙O的直径；②∠OGF=∠OCF；③若∠A=60°，则四边形OPFG是菱形；④直线EG是以BC为直径的外接圆的切线．其中正确的有（ ）
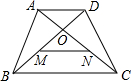如图，ABCD是等腰梯形，对角线AC与BD交于O点，AD=2，M、N分别是OB、OC的中点，AN与DM互相平分，则BC等于（ ）