题目内容
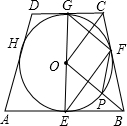 如图,⊙O是等腰梯形ABCD的内切圆,切点分别为E,F,G,H,其中AB∥CD,连接OB交⊙O于点P,连接OC,OG,OE,FG,FP,下列结论:①EG为⊙O的直径;②∠OGF=∠OCF;③若∠A=60°,则四边形OPFG是菱形;④直线EG是以BC为直径的外接圆的切线.其中正确的有( )
如图,⊙O是等腰梯形ABCD的内切圆,切点分别为E,F,G,H,其中AB∥CD,连接OB交⊙O于点P,连接OC,OG,OE,FG,FP,下列结论:①EG为⊙O的直径;②∠OGF=∠OCF;③若∠A=60°,则四边形OPFG是菱形;④直线EG是以BC为直径的外接圆的切线.其中正确的有( )| A、①②③④ | B、①②③ | C、①②④ | D、①③④ |
分析:连接OF,根据切线的性质,切线长定理逐一判断.
解答: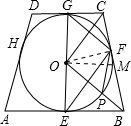 解:①∵CD、AB为⊙O的切线,∴OG⊥CD,OE⊥AB,又CD∥AB,∴O、E、G三点共线,即EG为直径,正确;
解:①∵CD、AB为⊙O的切线,∴OG⊥CD,OE⊥AB,又CD∥AB,∴O、E、G三点共线,即EG为直径,正确;
②连接OF,根据切线长定理可知,CG=CF,∴∠OCF=∠OCG,
又OF=OG,∴OC垂直平分FG,
∴∠OCG+∠CGF=90°,又∠OGF+∠CGF=90°,故∠OGF=∠OCF,正确;
∴③∠A=60时,根据等腰梯形的性质可知∠EBF=60°,根据切线长定理可知BO平分∠EBF,即∠OBF=30°,
又OF⊥BF,∴∠BOF=60°,故△OPF为等边三角形,又∠EOB=∠FOB=60°,可得△OFG为等边三角形,
∴四边形OPFG为菱形,正确;
④如图,过O点作OM∥AB交BC于点M,则OM为梯形BCGE的中位线,
∴BM=CM=
BC,OM=
(BE+CG)=
(BF+CF)=
BC,即BM=CM=OM,
又∵BE⊥EG,∴OM⊥EG,∴直线EG是以BC为直径的外接圆的切线,正确.
①②③④都正确,故选A.
 解:①∵CD、AB为⊙O的切线,∴OG⊥CD,OE⊥AB,又CD∥AB,∴O、E、G三点共线,即EG为直径,正确;
解:①∵CD、AB为⊙O的切线,∴OG⊥CD,OE⊥AB,又CD∥AB,∴O、E、G三点共线,即EG为直径,正确;②连接OF,根据切线长定理可知,CG=CF,∴∠OCF=∠OCG,
又OF=OG,∴OC垂直平分FG,
∴∠OCG+∠CGF=90°,又∠OGF+∠CGF=90°,故∠OGF=∠OCF,正确;
∴③∠A=60时,根据等腰梯形的性质可知∠EBF=60°,根据切线长定理可知BO平分∠EBF,即∠OBF=30°,
又OF⊥BF,∴∠BOF=60°,故△OPF为等边三角形,又∠EOB=∠FOB=60°,可得△OFG为等边三角形,
∴四边形OPFG为菱形,正确;
④如图,过O点作OM∥AB交BC于点M,则OM为梯形BCGE的中位线,
∴BM=CM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又∵BE⊥EG,∴OM⊥EG,∴直线EG是以BC为直径的外接圆的切线,正确.
①②③④都正确,故选A.
点评:本题考查了切线的性质,切线长定理,切线的判定定理,等腰梯形的性质及梯形中位线定理.具有一定的综合性,解题时,要根据要根据每个结论的要求,合理地选择所需要的性质或判断.

练习册系列答案
相关题目

 13、如图,P是等腰梯形ABCD上底AD上一点,若∠A=∠BPC,则图中与△ABP相似的所有三角形是
13、如图,P是等腰梯形ABCD上底AD上一点,若∠A=∠BPC,则图中与△ABP相似的所有三角形是
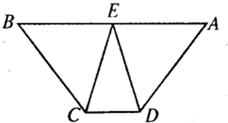 21、如图,E是等腰梯形ABCD底边AB上的中点,求证:DE=CE.
21、如图,E是等腰梯形ABCD底边AB上的中点,求证:DE=CE.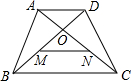 如图,ABCD是等腰梯形,对角线AC与BD交于O点,AD=2,M、N分别是OB、OC的中点,AN与DM互相平分,则BC等于( )
如图,ABCD是等腰梯形,对角线AC与BD交于O点,AD=2,M、N分别是OB、OC的中点,AN与DM互相平分,则BC等于( )