Question

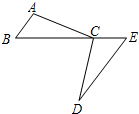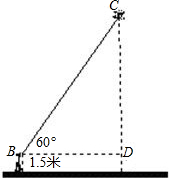
（1）已知：如图，C为BE上一点，点A，D分别在BE两侧．AB∥ED，AB=CE，BC=ED．求证：AC=CD．
（2）小明站在A处放风筝，风筝飞到C处时的线长为20米，这时测得∠CBD=60°，若牵引底端B离地面1.5米，求此时风筝离地面高度．（计算结果精确到0.1米，

3

≈1.732）

Answer 1

分析：（1）证明△ABC≌△CED即可；
（2）在直角三角形中利用勾股定理求得风筝距离牵引点的垂直高度后加上牵引点距地面的高度即能得到风筝距离地面的高度．

解答：（1）证明：∵AB∥ED，
∴∠ABC=∠CED，
∴在△ABC与△CED中，

AB=CE ∠ABC=∠CED BC=ED

∴△ABC≌△CED，
∴AC=CD．

（2）解：∵风筝飞到C处时的线长为20米，这时测得∠CBD=60°，
∴在Rt△ABC中，DC=BC×sin∠CBD=20×

3

2

=10

3

，
∴CE=CD+DE=10

3

+1.5≈17.32+1.5≈18.8m．
∴风筝距离地面的高度约为18.8米．

点评：本题考查了全等三角形及解直角三角形的相关知识，是一道比较典型的综合题，题目难度适中．