题目内容
如图，以Rt△ABC为直径分别向外作半圆，若S1=10，S3=8，则S2=
- A.2
- B.6
- C.
- D.
A
分析：根据勾股定理，得：AB2+BC2=AB2，再根据圆面积公式，可以证明：S1+S2=S3．即S2=10-8=2．
解答：∵AB2+BC2=AB2，S1=
•π（
）2=
；
S2=π（
）2=
；
S3=π（
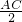）2=
；
S2+S3=+=
（AB2+BC2）==S1，
故S2=S1-S3=10-8=2．
故选A．
点评：注意根据圆面积公式结合勾股定理证明：S1+S2=S3，即直角三角形中，以直角边为直径的两个半圆面积的和等于以斜边为直径的半圆面积．
分析：根据勾股定理，得：AB2+BC2=AB2，再根据圆面积公式，可以证明：S1+S2=S3．即S2=10-8=2．
解答：∵AB2+BC2=AB2，S1=
•π（）2=；S2=
π（）2=；S3=
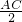π（）2=；S2+S3=
+=（AB2+BC2）==S1，故S2=S1-S3=10-8=2．
故选A．
点评：注意根据圆面积公式结合勾股定理证明：S1+S2=S3，即直角三角形中，以直角边为直径的两个半圆面积的和等于以斜边为直径的半圆面积．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
23、如图，以Rt△ABC的直角边AB为直径的半圆O，与斜边AC交于D，E是BC边上的中点，连接ED、BD．
如图，以Rt△ABC各边为直径的三个半圆围成两个新月形（阴影部分），已知AC=3cm，BC=4cm．则新月形（阴影部分）的面积和是
已知，如图，以Rt△ABC的斜边AB为直径作⊙0，D是BC上的点，且有弧AC=弧CD，连CD、BD，在BD延长线上取一点E，使∠DCE=∠CBD．
如图，以Rt△ABC的直角边AC为直径作圆O交斜边AB于点D，若劣弧CD=120°，则
（2009•黔南州）如图，以Rt△ABC的直角边AB为直径的半圆O，与斜边AC交于D，E是BC边上的中点，连接DE．