题目内容
 如图,以Rt△ABC的直角边AC为直径作圆O交斜边AB于点D,若劣弧CD=120°,则
如图,以Rt△ABC的直角边AC为直径作圆O交斜边AB于点D,若劣弧CD=120°,则| BD | AD |
3
3
.分析:如图,连接OD、CD.利用圆周角定理可以推知∠ADC=90°,由已知条件证得∠COD=120°;然后根据等边三角形的判定与性质可以求得∠A=60°,由直角三角形的两个锐角互余知∠ACD=∠ABC=30°;最后在直角三角形中,由“30°所对的直角边是斜边的一半”分别求得AD、BD与线段AC的数量关系,从而求得
的值.
| BD |
| AD |
解答: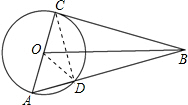 解:如图,连接OD、CD.
解:如图,连接OD、CD.
∵AC是⊙O的直径,
∴∠ADC=90°(直径所对的圆周角是直角);
又∵劣弧CD=120°,∴∠COD=120°,
∴∠OAD=60°;
∵OA=OD,
∴△OAD是等边三角形,
∴∠A=60°;
在Rt△CAD中,AD=
AC(30°所对的直角边是斜边的一半);
在Rt△ABC中,AC=
AB(30°所对的直角边是斜边的一半);
∴BD=AB-AD=
AC,
∴
=3.
故答案是:3.
 解:如图,连接OD、CD.
解:如图,连接OD、CD.∵AC是⊙O的直径,
∴∠ADC=90°(直径所对的圆周角是直角);
又∵劣弧CD=120°,∴∠COD=120°,
∴∠OAD=60°;
∵OA=OD,
∴△OAD是等边三角形,
∴∠A=60°;
在Rt△CAD中,AD=
| 1 |
| 2 |
在Rt△ABC中,AC=
| 1 |
| 2 |
∴BD=AB-AD=
| 3 |
| 2 |
∴
| BD |
| AD |
故答案是:3.
点评:本题综合考查了圆周角定理、含30°角的直角三角形以及等边三角形的判定与性质.解题时,通过作辅助线连接OD、CD构建等边△AOD和Rt△CAD来求得∠A的度数的.

练习册系列答案
相关题目
 23、如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连接ED、BD.
23、如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连接ED、BD. 如图,以Rt△ABC各边为直径的三个半圆围成两个新月形(阴影部分),已知AC=3cm,BC=4cm.则新月形(阴影部分)的面积和是
如图,以Rt△ABC各边为直径的三个半圆围成两个新月形(阴影部分),已知AC=3cm,BC=4cm.则新月形(阴影部分)的面积和是 已知,如图,以Rt△ABC的斜边AB为直径作⊙0,D是BC上的点,且有弧AC=弧CD,连CD、BD,在BD延长线上取一点E,使∠DCE=∠CBD.
已知,如图,以Rt△ABC的斜边AB为直径作⊙0,D是BC上的点,且有弧AC=弧CD,连CD、BD,在BD延长线上取一点E,使∠DCE=∠CBD. (2009•黔南州)如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连接DE.
(2009•黔南州)如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连接DE.