题目内容
在直角坐标系xOy中:(1)画出一次函数y=
| ||
| 2 |
| ||
| 2 |
(2)画出△ABC,使BC在x轴上,点A在直线a上(点A在第一象限),且BC=2,∠ABC=120°;
(3)写出点A、B、C的坐标;
(4)将△ABC绕点B在直角坐标平面内旋转,使点A落在x
 轴上,求此时过点A、B、C的抛物线的解析式.
轴上,求此时过点A、B、C的抛物线的解析式.
分析:(1)分别令x=0,y=0找出直线与两坐标轴的交点即可画出一次函数y=
x+
的图象.
(2)在x轴上找点C,使BC=2,根据∠ABC=120°可知,C在B的右侧,且B点坐标为(1,0),在直线y=
x+
的图象上取点A,使∠ABC=120°即可.
(3)过A作AD⊥x轴,根据锐角三角函数的定义即可求出P点的坐标.
(4)根据旋转的性质当A落到x轴上时,设此点为A′则AA′=AC,此时AC旋转的角度为∠ACD=60°,同理,B也旋转了60°,BC=B′C,过B′作B′E⊥x轴,根据锐角三角函数值的定义可知B′此时正好落在y轴上,根据两点间的距离公式可求出B′、A′的坐标,再用待定系数法即可求出过点A、B、C的抛物线的解析式.
| ||
| 2 |
| ||
| 2 |
(2)在x轴上找点C,使BC=2,根据∠ABC=120°可知,C在B的右侧,且B点坐标为(1,0),在直线y=
| ||
| 2 |
| ||
| 2 |
(3)过A作AD⊥x轴,根据锐角三角函数的定义即可求出P点的坐标.
(4)根据旋转的性质当A落到x轴上时,设此点为A′则AA′=AC,此时AC旋转的角度为∠ACD=60°,同理,B也旋转了60°,BC=B′C,过B′作B′E⊥x轴,根据锐角三角函数值的定义可知B′此时正好落在y轴上,根据两点间的距离公式可求出B′、A′的坐标,再用待定系数法即可求出过点A、B、C的抛物线的解析式.
解答:解:(1)令x=0,则y=
,令y=0,则x=-1,则函数图象与两坐标轴的交点分别为(0,
),(-1,0)
(2)因为C在x轴上,且∠ABC=120°,
所以B点坐标为(1,0),在直线y=
x+
的图象上取点A,使∠ABC=120°即可.
(3)设A(x,y),则y=
x+
,过A作AD⊥x轴,
则CD=x-1,∠ACD=180°-∠ABC=180°-120°=60°,
所以AD=CD•tan60°=
(x-1),
即
(x-1)=
x+
,
解得x=3,y=
×3+
=2
.
由(2)(3)可知A、B、C三点的坐标分别为:A(3,2
),B(-1,0),C(-1,0).
(4)设三角形旋转以后的图形为△A′B′C,
根据旋转的性质可知A′C=AC,B′C=BC,
此时AC旋转的角度为∠ACD=60°,
同理,B也旋转了60°,即∠ACA′=∠BCB′=60°,A′C=AC=
=4,
故A点坐标为(5,0),同理可得B′C=BC=
=2,
过B′作B′E⊥x轴,根据锐角三角函数的定义可知
EC=1,
故E与原点重合.
此时B′点坐标为(0,
)
设此时过点A、B、C的抛物线的解析式为:
y=ax2+bx+c,
把A′,B′,C三点坐标分别代入得,
,
解得:
,
故此函数的解析式为y=
x2-
x+
.
| ||
| 2 |
| ||
| 2 |
(2)因为C在x轴上,且∠ABC=120°,
所以B点坐标为(1,0),在直线y=
| ||
| 2 |
| ||
| 2 |
(3)设A(x,y),则y=
| ||
| 2 |
| ||
| 2 |
则CD=x-1,∠ACD=180°-∠ABC=180°-120°=60°,
所以AD=CD•tan60°=
| 3 |
即
| 3 |
| ||
| 2 |
| ||
| 2 |
解得x=3,y=
| ||
| 2 |
| ||
| 2 |
| 3 |
由(2)(3)可知A、B、C三点的坐标分别为:A(3,2
| 3 |
(4)设三角形旋转以后的图形为△A′B′C,
根据旋转的性质可知A′C=AC,B′C=BC,
此时AC旋转的角度为∠ACD=60°,
同理,B也旋转了60°,即∠ACA′=∠BCB′=60°,A′C=AC=
(1-3)2+(2
|
故A点坐标为(5,0),同理可得B′C=BC=
| (-1-1)2 |

过B′作B′E⊥x轴,根据锐角三角函数的定义可知
EC=1,
故E与原点重合.
此时B′点坐标为(0,
| 3 |
设此时过点A、B、C的抛物线的解析式为:
y=ax2+bx+c,
把A′,B′,C三点坐标分别代入得,
|
解得:
|
故此函数的解析式为y=
| ||
| 5 |
| 6 |
| 5 |
| 3 |
| 3 |
点评:此题比较复杂,涉及到一次函数图象上点的坐标特点,旋转的性质,二次函数图象上点的坐标特征及锐角三角函数值的定义.

练习册系列答案
相关题目

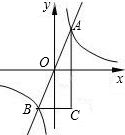 在直角坐标系xoy中,函数y=4x的图象与反比例函数y=
在直角坐标系xoy中,函数y=4x的图象与反比例函数y= (2012•北京二模)已知:如图,在直角坐标系xOy中,点A(8,0)、B(0,6),点C在x轴的负半轴上,AB=AC.动点M在x轴上从点C向点A移动,动点N在线段AB上从点A向点B移动,点M、N同时出发,且移动的速度都为每秒1个单位,移动时间为t秒(0<t<10).
(2012•北京二模)已知:如图,在直角坐标系xOy中,点A(8,0)、B(0,6),点C在x轴的负半轴上,AB=AC.动点M在x轴上从点C向点A移动,动点N在线段AB上从点A向点B移动,点M、N同时出发,且移动的速度都为每秒1个单位,移动时间为t秒(0<t<10). 析式为y=x2-mx+n.方程x2-mx+n=0的两根倒数和为-4.
析式为y=x2-mx+n.方程x2-mx+n=0的两根倒数和为-4.