题目内容
如图,在半径为5的圆O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为 ; 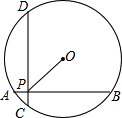


试题分析:作OM⊥AB于M,ON⊥CD于N,连接OP,OB,OD,由垂径定理、勾股定理得:OM=ON=
 =3,∵弦AB、CD互相垂直,∴∠DPB=90°,∵OM⊥AB于M,ON⊥CD于N,∴∠OMP=∠ONP=90°,∴四边形MONP是正方形,∴OP=
=3,∵弦AB、CD互相垂直,∴∠DPB=90°,∵OM⊥AB于M,ON⊥CD于N,∴∠OMP=∠ONP=90°,∴四边形MONP是正方形,∴OP=
点评:该题主要考查学生勾股定理的应用,结合了圆,以及弦的用法,需要学生灵活变动。

练习册系列答案
相关题目
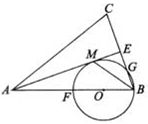
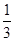 时,求⊙O的半径.
时,求⊙O的半径. 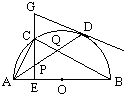
 ,OP=2,则AC的长是( )
,OP=2,则AC的长是( )




