Question

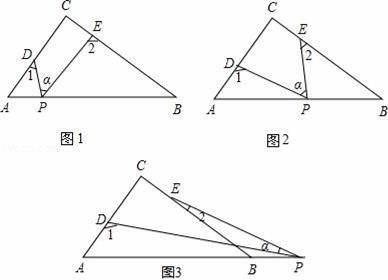
在△ABC中，∠C=90°，点D、E分别是边A以、BC上的点，点P是一动点，连接PD、PE，∠PDA=∠1，∠PEB=∠2，∠DPE=∠α．

（1）如图1所示，若点P在线段AB上，且∠α=40°，则∠1+∠2=　130　°；

（2）如图2所示，若点P在边AB上运动，则∠α、∠1、∠2之间的关系为有何数量关系；猜想结论并说明理由；

（3）如图3所示，若点P运动到边AB的延长线上，则∠α、∠1、∠2之间有何数量关系？猜想结论并说明理由．

Answer 1

【考点】三角形内角和定理；三角形的外角性质．

【专题】动点型．

【分析】（1）根据四边形内角和定理以及邻补角的定义得出∠1+∠2=∠C+∠α，进而得出即可；

（2）利用（1）中所求得出答案即可；

（3）利用三角外角的性质得出∠1=∠C+∠2+α=90°+∠2+α；

【解答】解：（1）∵∠1+∠2+∠CDP+∠CEP=360°，∠C+∠α+∠CDP+∠CEP=360°，

∴∠1+∠2=∠C+∠α，

∵∠C=90°，∠α=40°，

∴∠1+∠2=130°；

故答案为：130°；                                

（2）由（1）得出：

∠α+∠C=∠1+∠2，

∴∠1+∠2=90°+α

故答案为：∠1+∠2=90°+α；

（3）∠1=90°+∠2+α，

理由：∵∠2+∠α=∠DME，∠DME+∠C=∠1，

∴∠1=∠C+∠2+α=90°+∠2+α．

【点评】本题考查了三角形内角和定理和外角的性质、对顶角相等的性质，熟练利用三角形外角的性质是解题的关键．