题目内容
在数轴上,实数a、b的位置如图所示,则|a-b|-
的值是( )

| a2 |

分析:根据数轴表示数的方法得到a<0<b,根据二次根式的性质得到原式=|a-b|-|a|,再根据绝对值的意义得到原式=-(a-b)-(-a),然后去括号合并即可.
解答:解:∵a<0<b,
∴原式=|a-b|-|a|
=-(a-b)-(-a)
=-a+b+a
=b.
故选C.
∴原式=|a-b|-|a|
=-(a-b)-(-a)
=-a+b+a
=b.
故选C.
点评:本题考查了二次根式的性质:
=|a|.也考查了绝对值的意义和数轴.
| a2 |

练习册系列答案
相关题目
 如图,在数轴上表示实数
如图,在数轴上表示实数| 15 |
| A、点P | B、点Q | C、点M | D、点N |
已知x2=3,那么在数轴上与实数x对应的点可能是( )


| A、P1 | B、P4 | C、P2或P3 | D、P1或P4 |
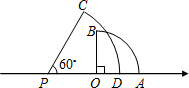 以数轴上的原点O为圆心,3为半径的扇形中,圆心角∠AOB=90°,另一个扇形是以点P为圆心,5为半径,圆心角∠CPD=60°,点P在数轴上表示实数a,如图.如果两个扇形的圆弧部分(
以数轴上的原点O为圆心,3为半径的扇形中,圆心角∠AOB=90°,另一个扇形是以点P为圆心,5为半径,圆心角∠CPD=60°,点P在数轴上表示实数a,如图.如果两个扇形的圆弧部分(
 如图,在数轴上表示实数
如图,在数轴上表示实数