题目内容
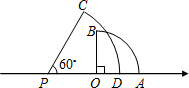以数轴上的原点O为圆心，3为半径的扇形中，圆心角∠AOB=90°，另一个扇形是以点P为圆心，5为半径，圆心角∠CPD=60°，点P在数轴上表示实数a，如图．如果两个扇形的圆弧部分（ |
| AB |
|
| CD |
分析：两扇形的圆弧相交，介于D、A两点重合与C、B两点重合之间，分别求出此时PD的长，PC的长，确定a的取值范围．
解答：解：当A、D两点重合时，PO=PD-OD=5-3=2，此时P点坐标为a=-2，
当B在弧CD时，由勾股定理得，PO=
=
=4，此时P点坐标为a=-4，
则实数a的取值范围是-4≤a≤-2．
故答案为：-4≤a≤-2．
当B在弧CD时，由勾股定理得，PO=
| PB2-OB2 |
| 52-32 |
则实数a的取值范围是-4≤a≤-2．
故答案为：-4≤a≤-2．
点评：本题考查了圆与圆的位置关系，实数与数轴的关系．关键是找出两弧相交时的两个重合端点．
练习册系列答案
名校课堂系列答案
相关题目
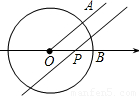
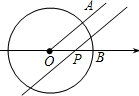如图，已知⊙O是以数轴的原点O为圆心，半径为1的圆，∠AOB=45°，点P在数轴上运动，若过点P且与OA平行的直线与⊙O有公共点，设OP=x，则x的取值范围是（ ）A、O＜x≤
| ||||
B、-
| ||||
| C、-1≤x≤1 | ||||
D、x＞
|
如图，已知⊙O是以数轴的原点O为圆心，半径为1的圆，∠AOB=45°，点P（P与O不重合）在数轴上运动，若过点P且与OA平行的直线与⊙O有公共点，设点P所表示的实数为x，则x的取值范围是（ ）| A、-1≤x＜0或0＜x≤1 | ||||
B、0＜x≤
| ||||
C、-
| ||||
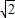D、x＞
|
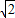
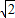
≤x≤
≤x≤
