题目内容
10．二次函数y=ax2+bx+c的图象恒在x轴上方的条件是（ ）| A． | a＞0，b2-4ac＞0 | B． | a＞0，b2-4ac＜0 | C． | a＜0，b2-4ac＞0 | D． | a＜0，b2-4ac＜0 |
分析 由于二次函数y=ax2+bx+c的图象在x轴上方，那么可以得到其开口方向，由此得到a的取值范围，同时也知道图象与x轴没有交点，由此即可得到判别式的取值范围，最后就可以得到二次函数y=ax2+bx+c的图象在x轴上方的条件．
解答 解：∵二次函数y=ax2+bx+c的图象在x轴上方，
∴开口要向上，并且图象与x轴没有交点，
∴二次函数y=ax2+bx+c的图象在x轴上方的条件是b2-4ac＜0，a＞0．
故选：B．
点评 此题考查抛物线与x轴的交点问题，掌握二次函数的性质，掌握开口方向与顶点坐标是解决问题的关键．
练习册系列答案
名校课堂系列答案
相关题目
15．
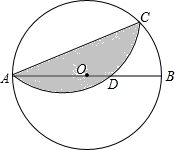如图，⊙O中，弦AC=$\sqrt{15}$，沿AC折叠劣弧$\widehat{AC}$交直径AB于D，DB=$\frac{1}{2}$，则直径AB=（ ）
如图，⊙O中，弦AC=$\sqrt{15}$，沿AC折叠劣弧$\widehat{AC}$交直径AB于D，DB=$\frac{1}{2}$，则直径AB=（ ）| A． | 4 | B． | $\frac{15}{4}$ | C． | 3$\sqrt{2}$ | D． | 2$\sqrt{5}$ |
19．一元二次方程x2-x-1=0的两个实数根中较大的根是（ ）
| A． | 1+$\sqrt{5}$ | B． | $\frac{1+\sqrt{5}}{2}$ | C． | $\frac{1-\sqrt{5}}{2}$ | D． | $\frac{-1+\sqrt{5}}{2}$ |
20．下列各组数中，数值相等的是（ ）
| A． | 32和23 | B． | -|23|和-|-2|3 | C． | -32和（-3）2 | D． | -（3×2）2和-3×22 |